题目内容
幂函数y=f(x)图象过点(2,
),则其单调增区间为 .
| 2 |
考点:幂函数的概念、解析式、定义域、值域
专题:函数的性质及应用
分析:由已知得y=x
,由此能求出幂函数y=f(x)的单调增区间.
| 1 |
| 2 |
解答:
解:∵幂函数y=f(x)=xa图象过点(2,
),
∴2a=
,解得a=
,
∴y=x
,
∴幂函数y=f(x)的单调增区间为[0,+∞).
故答案为:[0,+∞).
| 2 |
∴2a=
| 2 |
| 1 |
| 2 |
∴y=x
| 1 |
| 2 |
∴幂函数y=f(x)的单调增区间为[0,+∞).
故答案为:[0,+∞).
点评:本题考查幂函数的单调增区间的求法,是基础题,解题时要注意幂函数的性质的合理运用.

练习册系列答案
相关题目
如果如图撑血运行后,输出结果为132,那么程序中UNTIL,后面的条件应为( )


| A、i>11 | B、i≥11 |
| C、i≤11 | D、i<11 |
 有一个容量为200的样本,其频率分布直方图如图所示,据图估计,样本数据在[8,10)内的频数为
有一个容量为200的样本,其频率分布直方图如图所示,据图估计,样本数据在[8,10)内的频数为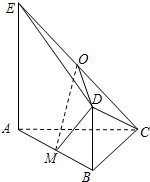 如图,平面ABDE⊥平面ABC,△ABC是等腰直角三角形,AC=BC=4,四边形ABDE是直角梯形,BD∥AE,BD⊥AB,BD=
如图,平面ABDE⊥平面ABC,△ABC是等腰直角三角形,AC=BC=4,四边形ABDE是直角梯形,BD∥AE,BD⊥AB,BD=