题目内容
一次函数y=kx+b，当k 0时，函数为增函数，当k 0时，函数是减函数．
考点：函数单调性的判断与证明
专题：阅读型
分析：在函数定义域内任意取2个实数x1和x2，且x1＜x2，在k＞0时、k＜0时，分别计算f（x1）-f（x2）的结果的符号．
解答：
解； 一次函数 y=f（x）=k x+b中，k≠0，在定义域内任意取2个实数x1和x2，且x1＜x2，
当k＞0时，f（x1）-f（x2）=（kx1+b ）-（kx2+b）=k（x1-x2）＜0，
f（x1）＜f（x2），∴f（x）在定义域内是增函数．
当k＜0时，f（x1）-f（x2）=（kx1+b ）-（kx2+b）=k（x1-x2）＞0
f（x1）＞f（x2），
∴f（x）在定义域内是减函数；
故答案为＞，＜．
当k＞0时，f（x1）-f（x2）=（kx1+b ）-（kx2+b）=k（x1-x2）＜0，
f（x1）＜f（x2），∴f（x）在定义域内是增函数．
当k＜0时，f（x1）-f（x2）=（kx1+b ）-（kx2+b）=k（x1-x2）＞0
f（x1）＞f（x2），
∴f（x）在定义域内是减函数；
故答案为＞，＜．
点评：用函数单调性的定义证明、判断函数的单调性．
练习册系列答案
快乐小博士巩固与提高系列答案
相关题目
两圆ρ=2cosθ，ρ=2sinθ的公共部分面积是（ ）
A、
| ||||
| B、π-2 | ||||
C、
| ||||
D、
|
已知点P（x，y）在以原点为圆心的单位圆上运动，则点Q（x+y，xy）的轨迹是（ ）
| A、圆 | B、抛物线 | C、椭圆 | D、双曲线 |
在港口
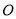正东方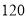
海里处，小岛
在港口
北偏东
方向和港口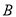
北偏西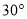
方向上，一艘科学考察船从港口O出发，沿北偏东
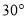的
方向以每小时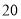
海里的速度驶离港口
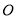，一艘快艇从港口B出发，以每小时
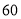海里的速度驶向小岛
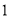小时，问快艇驶离港口
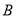后最少要经过多少时间才能和考察船相遇？
,
，则
等于（ ）
（B）
（C）
（D）
的实部为（ ）