题目内容
(1)证明:当a>1时,不等式a3+
>a2+
成立.
(2)要使上述不等式a3+
>a2+
成立,能否将条件“a>1”适当放宽?若能,请放宽条件并简述理由;若不能,也请说明理由.
(3)请你根据(1)、(2)的证明,试写出一个类似的更为一般的结论,且给予证明.
| 1 |
| a3 |
| 1 |
| a2 |
(2)要使上述不等式a3+
| 1 |
| a3 |
| 1 |
| a2 |
(3)请你根据(1)、(2)的证明,试写出一个类似的更为一般的结论,且给予证明.
考点:不等式的证明,类比推理
专题:证明题,分类讨论
分析:(1)用作差比较法证明不等式,把差化为因式积的形式,判断符号,得出结论.
(2)由于a-1与a5-1同号,对任何a>0且a≠1 恒成立,故上述不等式的条件可放宽为a>0且a≠1.
(3)左式-右式等于
(am-n-1)(am+n-1),根据m>n>0,分a>1 和0<a<1 两种情况讨论.
(2)由于a-1与a5-1同号,对任何a>0且a≠1 恒成立,故上述不等式的条件可放宽为a>0且a≠1.
(3)左式-右式等于
| 1 |
| nm |
解答:
解:(1)证明:a3+
-a2-
=
(a-1)(a5-1),∵a>1,∴
(a-1)(a5-1)>0,
∴原不等式成立.
(2)∵a-1与a5-1同号对任何a>0且a≠1 恒成立,∴上述不等式的条件可放宽为a>0且a≠1.
(3)根据(1)(2)的证明,可推知:若a>0且a≠1,m>n>0,则有am+
>an+
.
证:左式-右式=am-an+
-
=an(am-n -1)-
(am-n-1)
=(am-n-1)( an-
)=
(am-n-1)(am+n-1),
若a>1,则由m>n>0 可得
>0,am-n-1>0,am+n-1>0,∴不等式成立.
若0<a<1,则由m>n>0 可得
>0,0<am-n<1,0<am+n<1,∴不等式成立.
| 1 |
| a3 |
| 1 |
| a2 |
| 1 |
| a3 |
| 1 |
| a3 |
∴原不等式成立.
(2)∵a-1与a5-1同号对任何a>0且a≠1 恒成立,∴上述不等式的条件可放宽为a>0且a≠1.
(3)根据(1)(2)的证明,可推知:若a>0且a≠1,m>n>0,则有am+
| 1 |
| nm |
| 1 |
| nn |
证:左式-右式=am-an+
| 1 |
| nm |
| 1 |
| nn |
| 1 |
| am |
=(am-n-1)( an-
| 1 |
| am |
| 1 |
| am |
若a>1,则由m>n>0 可得
| 1 |
| am |
若0<a<1,则由m>n>0 可得
| 1 |
| am |
点评:本题考查不等式性质的应用,用比较法证明不等式,体现了分类讨论的数学思想,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知实数k满足
>1.则方程x2-kx+1=0的两个根可分别作为( )
| 1 |
| k-2 |
| A、一椭圆和一双曲线的离心率 |
| B、两抛物线的离心率 |
| C、一椭圆和一抛物线的离心率 |
| D、两椭圆的离心率 |
设f(x)是定义域为R的奇函数,且在(0,+∞)上是减函数,若f(1)=0,则不等式f(x)>0的解集是( )
| A、(-∞,-1)∪(1,+∞) |
| B、(-1,0)∪(0,1) |
| C、(-∞,-1)∪(0,1) |
| D、(-1,0)∪(1,+∞) |
两圆ρ=2cosθ,ρ=2sinθ的公共部分面积是( )
A、
| ||||
| B、π-2 | ||||
C、
| ||||
D、
|
空间四个不同的平面,它们有多种位置关系,从交线数目看,所有可能出现的交线数目的集合是( )
| A、{0,1,2,3,4,5,6} |
| B、{0,1,3,4,5,6} |
| C、{0,1,2,3,5,6} |
| D、{0,1,3,4} |
甲、乙、丙三个同学排成一排拍照,则甲排在中间的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
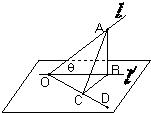 如图,l是平面α的斜线,斜足是O,A是l上任意一点,AB是平面α的垂线,B是垂足,设OD是平面α内与OB不同的一条直线,AC垂直于OD于C,若直线l与平面α所成的角θ=45°,∠BOC=45°,求∠AOC的大小.
如图,l是平面α的斜线,斜足是O,A是l上任意一点,AB是平面α的垂线,B是垂足,设OD是平面α内与OB不同的一条直线,AC垂直于OD于C,若直线l与平面α所成的角θ=45°,∠BOC=45°,求∠AOC的大小.