题目内容
求函数y=
（x＞2）的值域．
| 2x2-2x+1 |
| x2 |
考点：函数的值域
专题：函数的性质及应用
分析：整理原函数的解析式，利用换元法转化成二次函数，利用自变量的范围和二次函数的性质求得函数的值域．
解答：
解：y=
=2-
+
，
设t=
，则0＜t＜
，
则y=t2-2t+2=（t-1）2+1，
∴ymax=f（0）=2，ymin=f（
）=
，
∴函数的值域为（
，2）．
| 2x2-2x+1 |
| x2 |
| 2 |
| x |
| 1 |
| x2 |
设t=
| 1 |
| x |
| 1 |
| 2 |
则y=t2-2t+2=（t-1）2+1，
∴ymax=f（0）=2，ymin=f（
| 1 |
| 2 |
| 5 |
| 4 |
∴函数的值域为（
| 5 |
| 4 |
点评：本题主要考查了函数的值域的求法．换元法是解决函数值域问题的常用方法，应能熟练应用．
练习册系列答案
备战中考寒假系列答案
相关题目
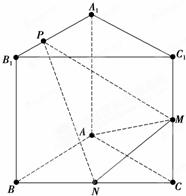如图，已知三棱柱ABC-A1B1C1的侧棱与底面垂直，AA1=AB=AC=1，AB⊥AC，M、N分别是CC1，BC的中点，点P在线段A1B1上，且