题目内容
已知向量
与向量
=（2，-1，2）共线，且满足
•
=18，（k
+
）⊥（k
-
），求向量
及k的值．
| b |
| a |
| a |
| b |
| a |
| b |
| a |
| b |
| b |
考点：数量积判断两个平面向量的垂直关系
专题：平面向量及应用
分析：由已知得存在实数λ，使
=λ
，由此能求出
=2
=（4，-2，4）．由（k
+
）⊥（k
-
），得（k2-4）|
|2=0，由此能求出k=±2．
| b |
| a |
| b |
| a |
| a |
| b |
| a |
| b |
| a |
解答：
解：∵
，
共线，∴存在实数λ，使
=λ
，
∴
•
=λ
2=λ|
|2，解得λ=2．
∴
=2
=（4，-2，4）．
∵（k
+
）⊥（k
-
），
∴（k
+
）•（k
-
）=（k
+2
）•（k
-2
）=0，
即（k2-4）|
|2=0，
解得k=±2．
| a |
| b |
| b |
| a |
∴
| a |
| b |
| a |
| a |
∴
| b |
| a |
∵（k
| a |
| b |
| a |
| b |
∴（k
| a |
| b |
| a |
| b |
| a |
| a |
| a |
| a |
即（k2-4）|
| a |
解得k=±2．
点评：本题考查向量
及k的值的求法，解题时要认真审题，注意向量共线和向量垂直的性质的合理运用．
| b |
练习册系列答案
名校课堂系列答案
相关题目
直线x+
y-m=0与圆x2+y2=1在第一象限内有两个不同的交点，则m的取值范围是（ ）
| 3 |
| A、（1，2） | ||
B、（
| ||
C、（1，
| ||
D、（
|
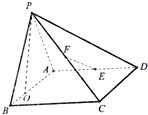如图，四棱锥P-ABCD的底面ABCD是矩形，平面PAB⊥平面ABCD，PA=AB=3，BC=2，E、F分别是棱AD、PC的中点．