题目内容
10.下列函数能用二分法求零点的是( )| A. | f(x)=x2 | B. | f(x)=$\sqrt{-{x^2}+1}$ | C. | f(x)=ln(x+2)2 | D. | f(x)=$\frac{1}{{|{{2^x}-3}|}}$ |
分析 根据二分法的定义,函数必须是连续函数,且函数在零点两侧的函数值异号,从而可得结论.
解答 解:对于A:f(x)=x2≥0恒成立,故不能用二分法求零点,
对于B:f(x)=$\sqrt{-{x^2}+1}$≥0恒成立,故不能用二分法求零点,
对于C,f(x)=ln(x+2)2,f(0)=ln4>0,f(-1)=0,f(-1.5)<ln$\frac{1}{4}$<0,故能用二分法求零点,
对于D:f(x)=$\frac{1}{{|{{2^x}-3}|}}$≥0恒成立,故不能用二分法求零点,
故选:C
点评 本题考查二分法的定义,理解函数必须是连续函数,且函数在零点两侧的函数值异号,属于基础题.

练习册系列答案
相关题目
1.等比数列{an}的前n项的和分别为Sn,S5=2,S10=6,则a16+a17+a18+a19+a20=( )
| A. | 24 | B. | 16 | C. | 12 | D. | 8 |
15.方程${x^2}=\sqrt{x}+3$的解所在的区间是( )
| A. | (0,1) | B. | (1,2) | C. | (2,3) | D. | (3,4) |
19.已知长方体同一个顶点的三条棱长分别为2,3,4,则该长方体的外接球的表面积等于( )
| A. | 13π | B. | 25π | C. | 29π | D. | 36π |
20.一货轮航行到M处,测得灯塔S在货轮的北偏东15°,与灯塔S相距20海里,随后货轮按北偏西30°的方向航行30分钟到达N处后,又测得灯塔在货轮的北偏东45°,则货轮的速度为( )
| A. | $20(\sqrt{3}+\sqrt{6})$海里/时 | B. | $20(\sqrt{6}-\sqrt{3})$海里/时 | C. | $20(\sqrt{2}+\sqrt{6})$海里/时 | D. | $20(\sqrt{6}-\sqrt{2})$海里/时 |
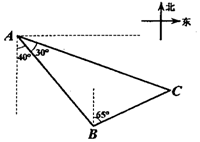 如图所示,一艘海轮从A处出发,以每小时40海里的速度沿南偏东40°方向直线航行,30分钟后到达B处,在C处有一座灯塔,海轮在A处观察灯塔,其方向是南偏东70°,在B处观察灯塔,其方向是北偏东65°,那么B、C两点间的距离是10$\sqrt{2}$海里.
如图所示,一艘海轮从A处出发,以每小时40海里的速度沿南偏东40°方向直线航行,30分钟后到达B处,在C处有一座灯塔,海轮在A处观察灯塔,其方向是南偏东70°,在B处观察灯塔,其方向是北偏东65°,那么B、C两点间的距离是10$\sqrt{2}$海里.