题目内容
18.已知幂函数y=f(x)的图象过点$(\frac{1}{2},\frac{{\sqrt{2}}}{2})$,则$log_2^{f(4)}$=1.分析 设幂函数y=f(x)=xα(α为常数),由图象过点$(\frac{1}{2},\frac{{\sqrt{2}}}{2})$,则$\frac{\sqrt{2}}{2}=(\frac{1}{2})^{α}$,解得α,再利用对数的运算性质即可得出.
解答 解:设幂函数y=f(x)=xα(α为常数),由图象过点$(\frac{1}{2},\frac{{\sqrt{2}}}{2})$,则$\frac{\sqrt{2}}{2}=(\frac{1}{2})^{α}$,解得α=$\frac{1}{2}$.
∴f(x)=$\sqrt{x}$,∴f(4)=2.
$log_2^{f(4)}$=log22=1.
故答案为:1.
点评 本题考查了幂函数的定义、对数函数的运算性质,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
6.函数y=sinx•cosx,x∈R的最小正周期为( )
| A. | 2 | B. | π | C. | 2π | D. | $\frac{1}{π}$ |
6.方程log2(x+2)=$\sqrt{-x}$的实数解的个数为( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
10.下列函数能用二分法求零点的是( )
| A. | f(x)=x2 | B. | f(x)=$\sqrt{-{x^2}+1}$ | C. | f(x)=ln(x+2)2 | D. | f(x)=$\frac{1}{{|{{2^x}-3}|}}$ |
7.下面四个推理,不属于演绎推理的是( )
| A. | 因为函数y=sinx(x∈R)的值域为[-1,1],2x-1∈R,所以y=sin(2x-1)(x∈R)的值域也为[-1,1] | |
| B. | 昆虫都是6条腿,竹节虫是昆虫,所以竹节虫有6条腿 | |
| C. | 在平面中,对于三条不同的直线a,b,c,若a∥b,b∥c则a∥c,将此结论放到空间中也是如此 | |
| D. | 如果一个人在墙上写字的位置与他的视线平行,那么,墙上字迹离地的高度大约是他的身高,凶手在墙上写字的位置与他的视线平行,福尔摩斯量得墙壁上的字迹距地面六尺多,于是,他得出了凶手身高六尺多的结论 |
 《中华人民共和国道路交通安全法》规定:车辆驾驶员血液酒精浓度在20一80 mg/l00mL(不含80)之间,属于酒后驾车;血液酒精浓度在80mg/l00mL(含80)以上时,属醉酒驾车.据有关调查,在一周内,某地区查处酒后驾车和醉酒驾车共300人.如图是对这300人血液中酒精含量进行检测所得结果的频率分布直方图,则属于醉酒驾车的人数约为( )
《中华人民共和国道路交通安全法》规定:车辆驾驶员血液酒精浓度在20一80 mg/l00mL(不含80)之间,属于酒后驾车;血液酒精浓度在80mg/l00mL(含80)以上时,属醉酒驾车.据有关调查,在一周内,某地区查处酒后驾车和醉酒驾车共300人.如图是对这300人血液中酒精含量进行检测所得结果的频率分布直方图,则属于醉酒驾车的人数约为( )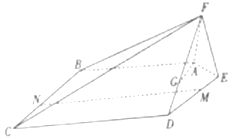 如图,在五棱锥F-ABCDE中,平面AEF⊥平面ABCDE,AF=EF=1,AB=DE=2,BC=CD=3,且∠AFE=∠ABC=∠BCD=∠CDE=90°.
如图,在五棱锥F-ABCDE中,平面AEF⊥平面ABCDE,AF=EF=1,AB=DE=2,BC=CD=3,且∠AFE=∠ABC=∠BCD=∠CDE=90°.