题目内容
已知直线l:(m-1)x+2my+2=0
(1)求证直线l必经过第四象限;
(2)若直线l不过第三象限,求实数m的取值范围;
(3)求直线l在两坐标轴上截距相等时的直线方程.
(1)求证直线l必经过第四象限;
(2)若直线l不过第三象限,求实数m的取值范围;
(3)求直线l在两坐标轴上截距相等时的直线方程.
考点:直线的截距式方程,确定直线位置的几何要素,直线的斜截式方程
专题:直线与圆
分析:(1)推导出直线l:(m-1)x+2my+2=0恒过定点(2,-1),由此能证明直线l必经过第四象限.
(2)把直线l:(m-1)x+2my+2=0化为斜截式方程,由直线l不过第三象限,得到直线l的斜率不大于0,在y轴上的截距不小于0,由此能求出实数m的取值范围.
(3)分别求出直线l:(m-1)x+2my+2=0的横截距和纵截距,令二者相等,能求出直线l的方程.
(2)把直线l:(m-1)x+2my+2=0化为斜截式方程,由直线l不过第三象限,得到直线l的斜率不大于0,在y轴上的截距不小于0,由此能求出实数m的取值范围.
(3)分别求出直线l:(m-1)x+2my+2=0的横截距和纵截距,令二者相等,能求出直线l的方程.
解答:
(1)证明:∵直线l:(m-1)x+2my+2=0,
∴(x+2y)m+(2-x)=0,
∴
,解得x=2,y=-1,
∴直线l:(m-1)x+2my+2=0恒过定点(2,-1),
∴直线l必经过第四象限.
(2)解:把直线l:(m-1)x+2my+2=0化为斜截式,得:
y=
x-
,
∵直线l不过第三象限,
∴直线l的斜率不大于0,在y轴上的截距不小于0,
即
,解得m<0.
∴实数m的取值范围是(-∞,0).
(3)解:直线l:(m-1)x+2my+2=0中,
令x=0,得y=-
;令y=0,得x=
,
∵直线l在两坐标轴上截距相等,
∴-
=
,解得m=-1,
∴直线l的方程为:x+y-1=0.
∴(x+2y)m+(2-x)=0,
∴
|
∴直线l:(m-1)x+2my+2=0恒过定点(2,-1),
∴直线l必经过第四象限.
(2)解:把直线l:(m-1)x+2my+2=0化为斜截式,得:
y=
| 1-m |
| 2m |
| 1 |
| m |
∵直线l不过第三象限,
∴直线l的斜率不大于0,在y轴上的截距不小于0,
即
|
∴实数m的取值范围是(-∞,0).
(3)解:直线l:(m-1)x+2my+2=0中,
令x=0,得y=-
| 1 |
| m |
| 2 |
| 1-m |
∵直线l在两坐标轴上截距相等,
∴-
| 1 |
| m |
| 2 |
| 1-m |
∴直线l的方程为:x+y-1=0.
点评:本题考查直线过第四象限的证明,考查直线不过第三象限时实数的取值范围的求法,考查直线方程的求法,解题时要认真审题,注意等价转化思想的合理运用.

练习册系列答案
相关题目
(2x-
)n的展开式的各个二项式系数之和为64,则在(2x-
)n的展开式中,常数项为( )
| 1 | ||
|
| 1 | ||
|
| A、-120 | B、120 |
| C、-60 | D、60 |
已知f(x)=lnx+x-2,g(x)=xlnx+x-2在(1,+∞)上都有且只有一个零点,f(x)的零点为x1,g(x)的零点为x2,则( )
| A、1<x2<x1<2 |
| B、1<x1<x2<2 |
| C、1<x1<2<x2 |
| D、2<x2<x1 |
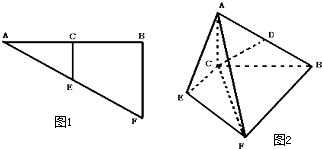 在Rt△ABF中,AB=2BF=4,C,E分别是AB,AF的中点(如图1).将此三角形沿CE对折,使平面AEC⊥平面BCEF(如图2),已知D是AB的中点.
在Rt△ABF中,AB=2BF=4,C,E分别是AB,AF的中点(如图1).将此三角形沿CE对折,使平面AEC⊥平面BCEF(如图2),已知D是AB的中点.