题目内容
已知f（x）=lnx+x-2，g（x）=xlnx+x-2在（1，+∞）上都有且只有一个零点，f（x）的零点为x1，g（x）的零点为x2，则（ ）
| A、1＜x2＜x1＜2 |
| B、1＜x1＜x2＜2 |
| C、1＜x1＜2＜x2 |
| D、2＜x2＜x1 |
考点：函数零点的判定定理
专题：函数的性质及应用
分析：函数f（x）=lnx+x-2的零点，即函数y=lnx与函数y=-x+2交点的横坐标，函数g（x）=xlnx+x-2的零点，即函数y=lnx与函数y=
=
-1交点的横坐标，在同一坐标系中做出函数y=lnx，函数y=-x+2与函数y=
-1的图象，数形结合可得答案．
| -x+2 |
| x |
| 2 |
| x |
| 2 |
| x |
解答：
解：函数f（x）=lnx+x-2的零点，即函数y=lnx与函数y=-x+2交点的横坐标，
函数g（x）=xlnx+x-2的零点，即函数y=lnx与函数y=
=
-1交点的横坐标，
在同一坐标系中做出函数y=lnx，函数y=-x+2与函数y=
-1的图象如下图所示：
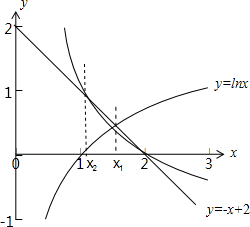
由图可得：1＜x2＜x1＜2，
故选：A
函数g（x）=xlnx+x-2的零点，即函数y=lnx与函数y=
| -x+2 |
| x |
| 2 |
| x |
在同一坐标系中做出函数y=lnx，函数y=-x+2与函数y=
| 2 |
| x |
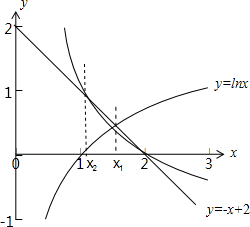
由图可得：1＜x2＜x1＜2，
故选：A
点评：本题考查函数图象的作法，熟练作出函数的图象是解决问题的关键，属中档题．
练习册系列答案
名师点睛字词句段篇系列答案
相关题目
已知函数f（x）=x3-tx2+3x，若对于任意的a∈[1，2]，b∈（2，3]，函数f（x）在区间（a，b）上单调递减，则实数t的取值范围是（ ）
| A、（-∞，3] |
| B、（-∞，5] |
| C、[3，+∞） |
| D、[5，+∞） |
下列函数中，在（0，+∞）上为减函数的是（ ）
A、y=
| ||
| B、y=（1-x）ex | ||
| C、y=x-ln（1+x） | ||
| D、y=x3-x |
设全集U=R，集合A={-2，-1}，B={x|（x+1）（x-2）＜0}，则A∩∁UB=（ ）
| A、{-2，-1} |
| B、{-2，1} |
| C、{-1，1} |
| D、{-2，-1，1} |
将函数f（x）=2sin（
+
）的图象向左平移
个单位，再向下平移1个单位，得到函数g（x）的图象，则g（x）的解析式为（ ）
| x |
| 3 |
| π |
| 6 |
| π |
| 4 |
A、g（x）=2sin（
| ||||
B、g（x）=2sin（
| ||||
C、g（x）=2sin（
| ||||
D、g（x）=2sin（
|
将一颗骰子连续投掷两次，两次正面出现点数之和能被4整除的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
已知x为第四象限角，则
-
=（ ）
|
|
| A、-2tanx |
| B、2tanx |
| C、2tanx或-2tanx |
| D、0 |