题目内容
已知椭圆C:
+
=1(a>b>0)的离心率与双曲线x2-y2=2的离心率互为倒数,且以抛物线y2=4x的焦点F为右焦点.
(I)求椭圆C的标准方程;
(II)过右焦点F作斜率为-
的直线l交曲线C于M、N两点,且
+
+
=0,又点H关于原点O的对称点为点G,试问M、G、N、H四点是否共圆?若共圆,求出圆心坐标和半径;若不共圆,请说明理由.
| x2 |
| a2 |
| y2 |
| b2 |
(I)求椭圆C的标准方程;
(II)过右焦点F作斜率为-
| ||
| 2 |
| OM |
| ON |
| OH |
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(I)双曲线x2-y2=2的离心率为
,可得椭圆C的离心率e=
=
.由抛物线y2=4x的焦点F(1,0)为椭圆的右焦点,可得c=1.再利用b2=a2-c2即可得出.
(II)设M(x1,y1),N(x2,y2),H(x0,y0),G(-x0,-y0).直线l的方程为:y=-
(x-1),与椭圆方程联立可得根与系数的关系,利用中点坐标公式可得线段MN的垂直平分线为:y-
=
(x-
),利用
+
+
=0,可得H,G.进而得到线段GH的垂直平分线.联立解得即可.
| 2 |
| ||
| 2 |
| c |
| a |
(II)设M(x1,y1),N(x2,y2),H(x0,y0),G(-x0,-y0).直线l的方程为:y=-
| ||
| 2 |
| ||
| 4 |
| 2 |
| 1 |
| 2 |
| OM |
| ON |
| OH |
解答:
解:(I)∵双曲线x2-y2=2的离心率为
,
∴椭圆C的离心率e=
=
.
∵抛物线y2=4x的焦点F(1,0)为椭圆的右焦点,∴c=1.
解得a=
,∴b2=a2-c2=1.
∴椭圆C的标准方程为
+y2=1.
(II)设M(x1,y1),N(x2,y2),H(x0,y0),G(-x0,-y0).
直线l的方程为:y=-
(x-1),
联立
,化为2x2-2x-1=0,
可得x1+x2=1,x1x2=-
.
∴y1+y2=-
(x1+x2-2)=
.
可得线段MN的垂直平分线为:y-
=
(x-
),
化为4
x-4y-
=0.
∵
+
+
=0,
∴x1+x2+x0=0,y1+y2+y0=0,
解得x0=-1,y0=-
,即H(-1,-
).
∴G(1,
).
线段GH垂直平分线的方程为y=-
x.
联立
,解得(
,-
),
∴r=
=
.
因此M、G、N、H四点是共圆,圆心坐标为(
,-
),半径r=
.
| 2 |
∴椭圆C的离心率e=
| ||
| 2 |
| c |
| a |
∵抛物线y2=4x的焦点F(1,0)为椭圆的右焦点,∴c=1.
解得a=
| 2 |
∴椭圆C的标准方程为
| x2 |
| 2 |
(II)设M(x1,y1),N(x2,y2),H(x0,y0),G(-x0,-y0).
直线l的方程为:y=-
| ||
| 2 |
联立
|
可得x1+x2=1,x1x2=-
| 1 |
| 2 |
∴y1+y2=-
| ||
| 2 |
| ||
| 2 |
可得线段MN的垂直平分线为:y-
| ||
| 4 |
| 2 |
| 1 |
| 2 |
化为4
| 2 |
| 2 |
∵
| OM |
| ON |
| OH |
∴x1+x2+x0=0,y1+y2+y0=0,
解得x0=-1,y0=-
| ||
| 2 |
| ||
| 2 |
∴G(1,
| ||
| 2 |
线段GH垂直平分线的方程为y=-
| 2 |
联立
|
| 1 |
| 8 |
| ||
| 8 |
∴r=
(1-
|
3
| ||
| 8 |
因此M、G、N、H四点是共圆,圆心坐标为(
| 1 |
| 8 |
| ||
| 8 |
3
| ||
| 8 |
点评:本题考查了圆锥曲线的标准方程及其性质、直线与椭圆相交问题转化为方程联立可得根与系数的关系、中点坐标公式、线段的垂直平分线性质,考查了推理能力与计算能力,属于难题.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
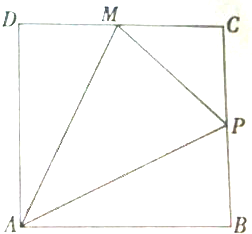 如图,动点P在边长为1的正方形ABCD上运动,点M为CD的中点,当点P沿A→B→C→M运动时,点P经过的路程设为x,△APM的面积为f(x),求f(x)的解析式.
如图,动点P在边长为1的正方形ABCD上运动,点M为CD的中点,当点P沿A→B→C→M运动时,点P经过的路程设为x,△APM的面积为f(x),求f(x)的解析式.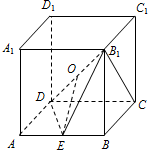 如图,在正方体ABCD-A1B1C1D1中,O,E分别为B1D,AB的中点.
如图,在正方体ABCD-A1B1C1D1中,O,E分别为B1D,AB的中点.