题目内容
用反证法证明“如果a＞b，那么
＞
”，假设内容应该是 ．
| 3 | a |
| 3 | b |
考点：反证法与放缩法
专题：证明题,反证法
分析：用反证法证明数学命题“如果a＞b，那么
＞
”时，应假设它的否定“
≤
”．
| 3 | a |
| 3 | b |
| 3 | a |
| 3 | b |
解答：
解：由于命题“
＞
”的否定为“
≤
”，
故用反证法证明命题“如果a＞b，那么
＞
”时，
应假设
≤
，
故答案为：
≤
．
| 3 | a |
| 3 | b |
| 3 | a |
| 3 | b |
故用反证法证明命题“如果a＞b，那么
| 3 | a |
| 3 | b |
应假设
| 3 | a |
| 3 | b |
故答案为：
| 3 | a |
| 3 | b |
点评：本题考查用反证法证明数学命题，求一个命题的否定的方法，得到命题“
＞
”的否定为“
≤
”，
是解题的关键．
| 3 | a |
| 3 | b |
| 3 | a |
| 3 | b |
是解题的关键．
练习册系列答案
相关题目
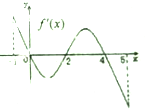已知函数f（x）的定义域为[-1，5]，部分对应值如下表．f（x）的导函数y=f′（x）的图象如图所示．下列关于函数f（x）的命题：①函数f（x）在[0，2]是减函数；②如果当x∈[-1，t]时，f（x）的最大值是2，那么t的最大值为4；③函数y=f（x）-a有4个零点时1＜a＜2．其中真命题的个数是（ ）