题目内容
20.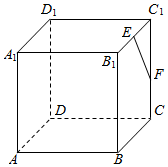 如图所示,在正方体ABCD-A1B1C1D1中,E、F分别是B1C1,CC1的中点.求:
如图所示,在正方体ABCD-A1B1C1D1中,E、F分别是B1C1,CC1的中点.求:(1)AB与DD1所成的角;
(2)AC与B1D1所成的角;
(3)AC与BC1所成的角;
(4)A1D与EF所成的角.
分析 (1)由DD1∥AA1,得∠A1AB是AB与DD1所成的角,由此能求出AB与DD1所成的角.
(2)由B1D1∥BD,正方形ABCD中,AC⊥BD,能求出AC与B1D1所成的角.
(3)由BC1∥AD1,得∠D1AC是AC与BC1所成的角,由此能求出AC与BC1所成的角.
(4)由EF∥B1C,A1D∥B1C,得EF∥A1D,由此能求出A1D与EF所成的角.
解答 解:(1)∵DD1∥AA1,
∴∠A1AB是AB与DD1所成的角,
∵A1A⊥AB,∴AB与DD1所成的角为90°.
(2)∵B1D1∥BD,正方形ABCD中,AC⊥BD,
∴AC与B1D1所成的角为90°.
(3)∵BC1∥AD1,
∴∠D1AC是AC与BC1所成的角,
∵AD1=AC=D1C,
∴∠D1AC=60°,
∴AC与BC1所成的角为60°.
(4)∵E、F分别是B1C1,CC1的中点,
∴EF∥B1C,
∵A1D∥B1C,
∴EF∥A1D,
∴A1D与EF所成的角为0°.
点评 本题考查异面直线所成角的求法,是基础题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
14.已知双曲线$\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{9}$=1的左右焦点分别为F1、F2,点P为双曲线上一点,△F1PF2的内切圆圆心为M,若S${\;}_{△{F}_{1}PM}$=S${\;}_{△{F}_{2}PM}$+8,那么S${\;}_{△{F}_{1}M{F}_{2}}$( )
| A. | 2$\sqrt{7}$ | B. | 6 | C. | 8 | D. | 10 |
14.已知p:a>4,q:方程$\frac{{x}^{2}}{4-a}$-$\frac{{y}^{2}}{1-a}$=1表示双曲线,则p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
15.若命题“?x∈[0,$\frac{π}{2}$],不等式exsinx≥kx”是真命题,则实数k的取值范围是( )
| A. | (-∞,1] | B. | (-∞,e${\;}^{\frac{π}{2}}$] | C. | (1,e${\;}^{\frac{π}{2}}$) | D. | [e${\;}^{\frac{π}{2}}$,+∞) |
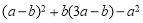 ,其中
,其中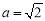 ,
,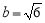 .
.