题目内容
9.函数f(x)=sin2x+cos2x的最大值为$\sqrt{2}$.分析 由三角函数公式化简可得f(x)=$\sqrt{2}$sin(2x+$\frac{π}{4}$),易得最大值.
解答 解:由三角函数公式化简可得f(x)=sin2x+cos2x
=$\sqrt{2}$($\frac{\sqrt{2}}{2}$sin2x+$\frac{\sqrt{2}}{2}$cos2x)=$\sqrt{2}$sin(2x+$\frac{π}{4}$),
∴当sin(2x+$\frac{π}{4}$)=1时,原函数取最大值$\sqrt{2}$.
故答案为:$\sqrt{2}$
点评 本题考查和差角的三角函数公式,涉及三角函数的最值,属基础题.

练习册系列答案
相关题目
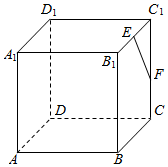 如图所示,在正方体ABCD-A1B1C1D1中,E、F分别是B1C1,CC1的中点.求:
如图所示,在正方体ABCD-A1B1C1D1中,E、F分别是B1C1,CC1的中点.求: 中,
中, ,以点
,以点 为圆心,
为圆心, 的长为半径作
的长为半径作 交
交 于点
于点 . 若
. 若 ,则阴影部分的面积为 _.
,则阴影部分的面积为 _.
 中,点
中,点 分别为线段
分别为线段 的中点.
的中点. 平面
平面 ;
; 在边
在边 上,
上, ,求证:
,求证: .
.
 的参数方程为
的参数方程为 (
( 为参数),以坐标原点为极点,
为参数),以坐标原点为极点, 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线 的极坐标方程为
的极坐标方程为 ,且曲线
,且曲线 的左焦点
的左焦点 在直线
在直线 上.
上. 与曲线
与曲线 交于
交于 两点,求
两点,求 的值;
的值; 的内接矩形的周长的最大值.
的内接矩形的周长的最大值.