题目内容
已知二次函数y=x2+4x-2,当a≤x≤a+1(其中a为参数)时,求y的最大值,最小值和相应的x值.
考点:二次函数的性质
专题:计算题,函数的性质及应用
分析:令f(x)=y=x2+4x-2=(x+2)2-6,讨论区间[a,a+1]与对称轴x=-2的位置关系,从而求最值及最值点.
解答:
解:令f(x)=y=x2+4x-2=(x+2)2-6;
①当a+1≤-2,即a≤-3时,
f(x)=x2+4x-2在[a,a+1]上是减函数,
故f(x)max=f(a)=(a+2)2-6,
f(x)min=f(a+1)=(a+3)2-6;
②当-2<a+1≤-1.5,即-3<a≤-2,5时,
f(x)=x2+4x-2在[a,-2]上是减函数,在[-2,a+1]上是增函数;
且a到-2的距离大于等于a+1到-2的距离;
故f(x)max=f(a)=(a+2)2-6,
f(x)min=f(-2)=-6;
③当-1.5<a+1<-1,即-2.5<a<-2时,
f(x)=x2+4x-2在[a,-2]上是减函数,在[-2,a+1]上是增函数;
且a到-2的距离小于a+1到-2的距离;
故f(x)max=f(a+1)=(a+3)2-6,
f(x)min=f(-2)=-6;
④当a+1≥-1,即a≥-2时,
f(x)=x2+4x-2在[a,a+1]上是增函数,
故f(x)max=f(a+1)=(a+3)2-6,
f(x)min=f(a)=(a+2)2-6.
①当a+1≤-2,即a≤-3时,
f(x)=x2+4x-2在[a,a+1]上是减函数,
故f(x)max=f(a)=(a+2)2-6,
f(x)min=f(a+1)=(a+3)2-6;
②当-2<a+1≤-1.5,即-3<a≤-2,5时,
f(x)=x2+4x-2在[a,-2]上是减函数,在[-2,a+1]上是增函数;
且a到-2的距离大于等于a+1到-2的距离;
故f(x)max=f(a)=(a+2)2-6,
f(x)min=f(-2)=-6;
③当-1.5<a+1<-1,即-2.5<a<-2时,
f(x)=x2+4x-2在[a,-2]上是减函数,在[-2,a+1]上是增函数;
且a到-2的距离小于a+1到-2的距离;
故f(x)max=f(a+1)=(a+3)2-6,
f(x)min=f(-2)=-6;
④当a+1≥-1,即a≥-2时,
f(x)=x2+4x-2在[a,a+1]上是增函数,
故f(x)max=f(a+1)=(a+3)2-6,
f(x)min=f(a)=(a+2)2-6.
点评:本题考查了二次函数的性质应用,属于中档题.

练习册系列答案
相关题目
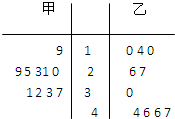 某林管部门在每年植树节前,为保证树苗的质量,都会对树苗进行检测.现从甲、乙两种树苗中各抽取10株,测量其高度,所得数据如茎叶图所示,则下列描述正确的是( )
某林管部门在每年植树节前,为保证树苗的质量,都会对树苗进行检测.现从甲、乙两种树苗中各抽取10株,测量其高度,所得数据如茎叶图所示,则下列描述正确的是( )| A、甲树苗的平均高度大于乙树苗的平均高度,且甲树苗比乙树苗长得整齐 |
| B、甲树苗的平均高度大于乙树苗的平均高度,但乙树苗比甲树苗长得整齐 |
| C、乙树苗的平均高度大于甲树苗的平均高度,但甲树苗比乙树苗长得整齐 |
| D、乙树苗的平均高度大于甲树苗的平均高度,且乙树苗比甲树苗长得整齐 |
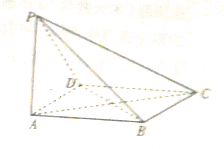 如图,四边形ABCD是菱形,PA⊥ABCD,AD=2,∠BAD=60°.
如图,四边形ABCD是菱形,PA⊥ABCD,AD=2,∠BAD=60°.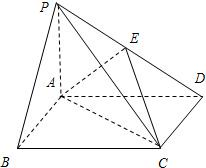 如图,在底面是矩形的四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB=2,BC=4.E是PD的中点,
如图,在底面是矩形的四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB=2,BC=4.E是PD的中点,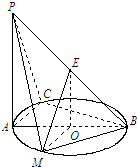 如图所示,PA⊥平面ABC,点C在以AB为直径的⊙O上,∠CBA=30°,PA=AB=2,点E为线段PB的中点,点M在弧AB上,且OM∥AC.
如图所示,PA⊥平面ABC,点C在以AB为直径的⊙O上,∠CBA=30°,PA=AB=2,点E为线段PB的中点,点M在弧AB上,且OM∥AC.