题目内容
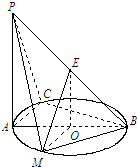 如图所示,PA⊥平面ABC,点C在以AB为直径的⊙O上,∠CBA=30°,PA=AB=2,点E为线段PB的中点,点M在弧AB上,且OM∥AC.
如图所示,PA⊥平面ABC,点C在以AB为直径的⊙O上,∠CBA=30°,PA=AB=2,点E为线段PB的中点,点M在弧AB上,且OM∥AC.(1)求证:平面MOE∥平面PAC;
(2)求证:平面PAC⊥平面PCB;
(3)求三棱锥O-PBC的体积.
考点:棱柱、棱锥、棱台的体积,平面与平面平行的判定,平面与平面垂直的判定
专题:空间位置关系与距离
分析:(1)利用三角形的中位线定理可得OE∥PA.即可得出OE∥平面PAC.再利用OM∥AC,可得OM∥平面PAC.再利用面面平行的判定定理即可得出平面MOE∥平面PAC.
(2)点C在以AB为直径的⊙O上,可得BC⊥AC.利用PA⊥平面ABC,可得PA⊥BC.可得BC⊥平面PAC.即可得出平面PAC⊥平面PCB.
(3)利用V三棱锥O-PBC=V三棱锥P-OBC=
•S△OBC•PA即可得出.
(2)点C在以AB为直径的⊙O上,可得BC⊥AC.利用PA⊥平面ABC,可得PA⊥BC.可得BC⊥平面PAC.即可得出平面PAC⊥平面PCB.
(3)利用V三棱锥O-PBC=V三棱锥P-OBC=
| 1 |
| 3 |
解答:
(1)证明:∵点E为线段PB的中点,点O为线段AB的中点,
∴OE∥PA.
∵PA?平面PAC,OE?平面PAC,
∴OE∥平面PAC.
又∵OM∥AC,AC?平面PAC,OM?平面PAC,
∴OM∥平面PAC.
∵OE?平面MOE,OM?平面MOE,OE∩OM=O,
∴平面MOE∥平面PAC.
(2)证明:∵点C在以AB为直径的⊙O上,∴∠ACB=90°,即BC⊥AC.
∵PA⊥平面ABC,BC?平面ABC,
∴PA⊥BC.
∵PA∩AC=A,
∴BC⊥平面PAC.
∵BC?平面PBC,
∴平面PAC⊥平面PCB.
(3)V三棱锥O-PBC=V三棱锥P-OBC=
•S△OBC•PA=
×
×1×1×sin120°×2=
.
∴OE∥PA.
∵PA?平面PAC,OE?平面PAC,
∴OE∥平面PAC.
又∵OM∥AC,AC?平面PAC,OM?平面PAC,
∴OM∥平面PAC.
∵OE?平面MOE,OM?平面MOE,OE∩OM=O,
∴平面MOE∥平面PAC.
(2)证明:∵点C在以AB为直径的⊙O上,∴∠ACB=90°,即BC⊥AC.
∵PA⊥平面ABC,BC?平面ABC,
∴PA⊥BC.
∵PA∩AC=A,
∴BC⊥平面PAC.
∵BC?平面PBC,
∴平面PAC⊥平面PCB.
(3)V三棱锥O-PBC=V三棱锥P-OBC=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| ||
| 6 |
点评:本题考查了线面面面平行与垂直的判定与性质定理、三棱锥的体积计算公式、三角形的中位线定理,考查了推理能力与计算能力,考查了空间想象能力,属于中档题.

练习册系列答案
 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
已知(2+
)n(其中n∈N*)的展开式中含x3项的系数为14,则n=( )
| x |
| A、6 | B、7 | C、8 | D、9 |
某人午觉醒来,发现表停了,他打开收音机,想听电台报时,他等待的时间不多于10分钟的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|