题目内容
14.(理科做)用数学归纳法证明:$1+2+3+…+n=\frac{n(n+1)}{2}\;n∈{N^*}$.分析 用数学归纳法证明:(1)当n=1时,去证明等式成立;(2)假设当n=k时,等时成立,用上归纳假设后,去证明当n=k+1时,等式也成立即可.
解答 解:证明:(1)当n=1时,1=1,等式成立.
(2)假设当n=k时,有1+2+3+…+k=$\frac{1}{2}$k(k+1)成立.
那么,当n=k+1时,
1+2+3+…+k+k+1=$\frac{1}{2}$k(k+1)+(k+1)
=$\frac{1}{2}$(k+1)(k+2),
=$\frac{1}{2}$(k+1)[(k+1)+1],
∴当n=k+1时等式成立,
∴对任意的n∈N*,等式都成立.
点评 本题的考点是数学归纳法,主要考查数学归纳法的第二步,在假设的基础上,n=k+1时等式左边增加的项,关键是搞清n=k时,等式左边的规律,从而使问题得解,属于中档题.

练习册系列答案
相关题目
2.化简$2\sqrt{1-sin10}+\sqrt{2+2cos10}$的结果是( )
| A. | 4cos5-2sin5 | B. | -2sin5-4cos5 | C. | 2sin5-4cos5 | D. | -2sin5 |
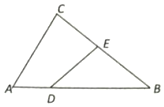 如图,在△ABC中,已知点D,E分别在边AB,BC上,且AB=3AD,BC=2BE.
如图,在△ABC中,已知点D,E分别在边AB,BC上,且AB=3AD,BC=2BE.