题目内容
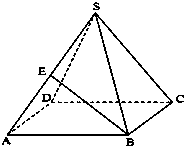
正四棱锥S-ABCD的侧棱长为
,底面边长为
,E为SA中点,求异面直线BE与SC所成的角的大小.
| 2 |
| 3 |

考点:异面直线及其所成的角
专题:空间角
分析:连接底面正方形ABCD对角线AC、BD,交于F,EF是三角形ASC的中位线,EF∥SC,EF与BE的成角是BE与SC的成角,由此能求出异面直线BE与SC所成角的大小.
解答:
解:连接底面正方形ABCD对角线AC、BD,交于F,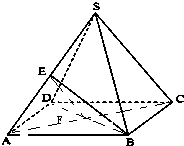
则F是AC和BD的中点,
连接EF,BD,EF是三角形ASC的中位线,EF∥SC,
且EF=
SC,则EF与BE的成角是BE与SC的成角,
BF=
,AB=
,EF=
,
三角形SAB是等腰三角形,从S作SG⊥AB,
cosA=
=
=
,
根据余弦定理,BE2=AE2+AB2-2AE•AB•cosA=2,BE=
,
在△BFE中根据余弦定理,
BF2=EF2+BE2-2EF•BEcos∠BEF,cos∠BEF=
,∴∠BEF=60°,
∴异面直线BE与SC所成角的大小60°.

则F是AC和BD的中点,
连接EF,BD,EF是三角形ASC的中位线,EF∥SC,
且EF=
| 1 |
| 2 |
BF=
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
三角形SAB是等腰三角形,从S作SG⊥AB,
cosA=
| AB |
| 2AS |
| ||
2
|
| ||
| 4 |
根据余弦定理,BE2=AE2+AB2-2AE•AB•cosA=2,BE=
| 2 |
在△BFE中根据余弦定理,
BF2=EF2+BE2-2EF•BEcos∠BEF,cos∠BEF=
| 1 |
| 2 |
∴异面直线BE与SC所成角的大小60°.
点评:本题考查异面直线所成角的大小的求法,是中档题,解题时要认真审题,注意余弦定理的合理运用.

练习册系列答案
相关题目
若a=0.63,b=log30.2,c=30.6,则( )
| A、c>a>b |
| B、a>c>b |
| C、c>b>a |
| D、b>c>a |
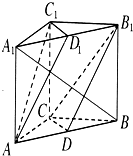 如图所示,在三棱柱ABC-A1B1C1中,AC=BC,AA1⊥平面ABC,点D,D1分别是AB,A1B1的中点.
如图所示,在三棱柱ABC-A1B1C1中,AC=BC,AA1⊥平面ABC,点D,D1分别是AB,A1B1的中点.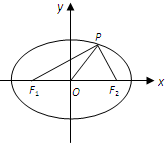 如图,F1,F2分别为椭圆
如图,F1,F2分别为椭圆 已知一四棱锥P-ABCD的三视图如图所示,E是側棱PC上的动点.
已知一四棱锥P-ABCD的三视图如图所示,E是側棱PC上的动点.