题目内容
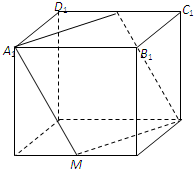 在棱长为a的正方体ABCD-A1B1C1D1中,M是棱AB的中点,过A1,M,C三点的平面交棱C1D1于N点,
在棱长为a的正方体ABCD-A1B1C1D1中,M是棱AB的中点,过A1,M,C三点的平面交棱C1D1于N点,(Ⅰ)求证:四边形A1MCN为平行四边形;
(Ⅱ)求直线CD1与平面A1MCN所成角的正弦值.
考点:异面直线及其所成的角,棱柱的结构特征
专题:空间位置关系与距离,空间角
分析:(Ⅰ)由已知条件推导出CM∥A1N,A1M∥CN,由此能证明四边形A1MCN为平行四边形.
(Ⅱ)延长CN、DD1交于点P,过D作DQ⊥AN,垂足为Q,连结PQ,过D1作D1H⊥PQ,垂足为H,连结CH,由D1H⊥平面A1MCN,知∠D1CH即为直线CD1与平面A1MCN所成角,由此能求出直线CD1与平面A1MCN所成角的正弦值.
(Ⅱ)延长CN、DD1交于点P,过D作DQ⊥AN,垂足为Q,连结PQ,过D1作D1H⊥PQ,垂足为H,连结CH,由D1H⊥平面A1MCN,知∠D1CH即为直线CD1与平面A1MCN所成角,由此能求出直线CD1与平面A1MCN所成角的正弦值.
解答:
(Ⅰ)证明:∵正方体ABCD-A1B1C1D1,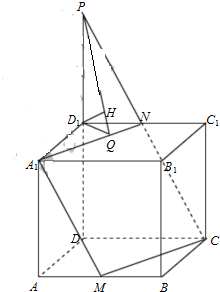
∴平面ABCD∥平面A1B1C1D1,
∵平面A1MCN∩平面ABCD=CM,
平面A1MCN∩平面A1B1C1D1=A1N,
∴CM∥A1N,同理,A1M∥CN,
∴四边形A1MCN为平行四边形.
(Ⅱ)解:延长CN、DD1交于点P,过D作DQ⊥AN,垂足为Q,
连结PQ,过D1作D1H⊥PQ,垂足为H,连结CH,
∵D1H⊥平面A1MCN,
∴∠D1CH即为直线CD1与平面A1MCN所成角,
在Rt△D1CH中,CD1=
a,D1H=
a,
∴sin∠D1CH=
=
,
∴直线CD1与平面A1MCN所成角的正弦值为
.

∴平面ABCD∥平面A1B1C1D1,
∵平面A1MCN∩平面ABCD=CM,
平面A1MCN∩平面A1B1C1D1=A1N,
∴CM∥A1N,同理,A1M∥CN,
∴四边形A1MCN为平行四边形.
(Ⅱ)解:延长CN、DD1交于点P,过D作DQ⊥AN,垂足为Q,
连结PQ,过D1作D1H⊥PQ,垂足为H,连结CH,
∵D1H⊥平面A1MCN,
∴∠D1CH即为直线CD1与平面A1MCN所成角,
在Rt△D1CH中,CD1=
| 2 |
| ||
| 6 |
∴sin∠D1CH=
| D1H |
| CD1 |
| ||
| 6 |
∴直线CD1与平面A1MCN所成角的正弦值为
| ||
| 6 |
点评:本题考查平行四边形的证明,考查直线与平面所成角的正弦值的求法,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
有一种细菌和一种病毒,每个细菌在每秒钟杀死一个病毒的同时将自身分裂为3个,现在有一个这样的细菌和110个这样的病毒,问细菌将病毒全部杀死至少需要( )
| A、4秒钟 | B、5秒钟 |
| C、6秒钟 | D、7秒钟 |
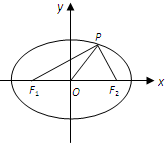 如图,F1,F2分别为椭圆
如图,F1,F2分别为椭圆 已知一四棱锥P-ABCD的三视图如图所示,E是側棱PC上的动点.
已知一四棱锥P-ABCD的三视图如图所示,E是側棱PC上的动点.