题目内容
15.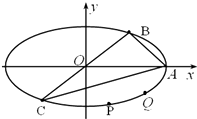 如图,椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的长轴长为4,点A,B,C为椭圆上的三个点,A为椭圆的右端点,BC过中心O,且|BC|=2|AB|,S△ABC=3.
如图,椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的长轴长为4,点A,B,C为椭圆上的三个点,A为椭圆的右端点,BC过中心O,且|BC|=2|AB|,S△ABC=3.(Ⅰ)求椭圆的标准方程;
(Ⅱ)设P,Q是椭圆上位于直线AC同侧的两个动点(异于A,C),且满足∠PBC=∠QBA,试讨论直线BP与直线BQ斜率之间的关系,并求直线PQ的斜率.
分析 (Ⅰ)由4a=4,则a=2,根据三角形的面积公式,求得B点坐标,代入椭圆方程,即可求得b的值,求得椭圆方程;
(Ⅱ)由题意可知:∠PBC=∠QBA,则kBP=-kBQ,设直线BP的方程,代入椭圆方程,利用韦达定理求得P点坐标,同理求得Q点坐标,直线PQ的斜率.
解答 解:(Ⅰ)由2a=4,则a=2,|BC|=2|AB|,S△OAB=$\frac{1}{2}$S△ABC=$\frac{3}{2}$.
由△AOB是等腰三角形,则B(1,$\frac{3}{2}$),将B代入椭圆方程,$\frac{1}{4}+\frac{9}{4{b}^{2}}=1$,解得:b2=3,
∴椭圆方程:$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$;
(Ⅱ)由题意可知:BP,BQ斜率存在,又∠PBC=∠QBA,
则kBP=-kBQ,
设直线BP:y-$\frac{3}{2}$=k(x-1),代入椭圆方程:$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$;
化简得:(3+4k2)x2-8k(k-$\frac{3}{2}$)x+4k2-12k-3=0,
由其一解为1,另一解为xP=$\frac{4{k}^{2}-12k-3}{3+4{k}^{2}}$,解得:yP=$\frac{-12{k}^{2}-6k}{3+4{k}^{2}}$+$\frac{3}{2}$,
用-k代入,解得:xQ=$\frac{4{k}^{2}+12k-3}{3+4{k}^{2}}$,yQ=$\frac{-12{k}^{2}+6k}{3+4{k}^{2}}$+$\frac{3}{2}$,
则直线PQ的斜率kPQ=$\frac{{y}_{P}-{y}_{Q}}{{x}_{P}-{x}_{Q}}$=$\frac{1}{2}$,
∴直线PQ的斜率为$\frac{1}{2}$.
点评 本题考查椭圆的标准方程及简单几何意义,直线与椭圆的位置关系,考查韦达定理及直线的斜率公式,考查计算能力,属于中档题.

| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
| A. | 2 | B. | -2 | C. | -2i | D. | 2或-2 |
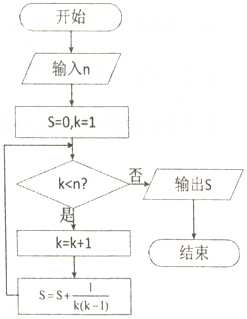
| A. | $\frac{1}{10}$ | B. | $\frac{8}{9}$ | C. | $\frac{9}{10}$ | D. | $\frac{10}{11}$ |
 菜农定期使用低害杀虫农药对蔬菜进行喷洒,以防止害虫的危害,但采集上市时蔬菜仍存有少量的残留农药,食用时需要用清水清洗干净,下表是用清水x(单位:千克) 清洗该蔬菜1千克后,蔬菜上残留的农药y(单位:微克) 的统计表:
菜农定期使用低害杀虫农药对蔬菜进行喷洒,以防止害虫的危害,但采集上市时蔬菜仍存有少量的残留农药,食用时需要用清水清洗干净,下表是用清水x(单位:千克) 清洗该蔬菜1千克后,蔬菜上残留的农药y(单位:微克) 的统计表:| x | 1 | 2 | 3 | 4 | 5 |
| y | 58 | 54 | 39 | 29 | 10 |
(2)若用解析式$\widehaty=c{x^2}+d$作为蔬菜农药残量$\widehaty$与用水量x的回归方程,令ω=x2,计算平均值$\overlineω$与$\overline y$,完成以下表格(填在答题卡中),求出$\widehaty$与x的回归方程.(c,d精确到0.1)
| ω | 1 | 4 | 9 | 16 | 25 |
| y | 58 | 54 | 39 | 29 | 10 |
| ${ω_i}-\overlineω$ | -10 | -7 | -2 | 5 | 14 |
| ${y_i}-\overline y$ | 20 | 16 | 1 | -28 |
估计需要用多少千克的清水清洗一千克蔬菜?(精确到0.1,参考数据$\sqrt{5}≈2.236$)
(附:线性回归方程$\widehaty=bx+a$中系数计算公式分别为;$b=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2}-n{{(\overline x)}^2}}}=\frac{{\sum_{i=1}^n{({x_i}-\overline x)({y_i}-\overline y})}}{{\sum_{i=1}^n{{{({x_i}-\overline x)}^2}}}}$,$a=\overline y-b\overline x$)
| 广告费用x(万元) | 8 | 3 | 4 | 5 |
| 销售额y(万元) | 54 | 26 | 39 | 41 |
| A. | 47.4 万元 | B. | 57.7万元 | C. | 49.4万元 | D. | 62.4万元 |