题目内容
2．已知两个圆的方程分别为x2+y2=4和x2+y2+2y-6=0，则它们的公共弦长为2$\sqrt{3}$．分析 求出公共弦方程，再利用垂径定理计算弦长．
解答 解：两圆方程相减得公共弦方程为y-1=0，
圆x2+y2=4的圆心为O（0，0），半径为r=2，
∴圆心O到公共弦的距离d=1，
∴两圆的公共弦长为2$\sqrt{{r}^{2}-{d}^{2}}$=2$\sqrt{3}$．
故答案为：2$\sqrt{3}$．
点评 本题考查了圆与圆的位置关系，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
11．对于函数y=sin（$\frac{13}{2}$π-x），下面说法中正确的是（ ）
| A． | 函数是周期为2π的偶函数 | B． | 函数是周期为π的偶函数 | ||
| C． | 函数是周期为2π的奇函数 | D． | 函数是周期为π的奇函数 |
8．阅读下面的程序框图，运行相应的程序，则输出的K和S的值分别为（ ）
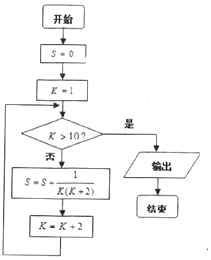
| A． | 9，$\frac{4}{9}$ | B． | 11，$\frac{5}{11}$ | C． | 11，$\frac{10}{11}$ | D． | 13，$\frac{12}{13}$ |
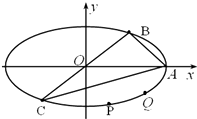如图，椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的长轴长为4，点A，B，C为椭圆上的三个点，A为椭圆的右端点，BC过中心O，且|BC|=2|AB|，S△ABC=3．
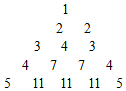观察如图所示的”三角数阵”