已知复数z满足(1+2i3)z=1+2i.则z的虚部是$\frac{4}{5}$．题目和参考答案——青夏教育精英家教网—

题目内容

10．已知复数z满足（1+2i³）z=1+2i，则z的虚部是$\frac{4}{5}$．

分析把已知等式变形，再由复数代数形式的乘除运算化简得答案．

解答解：由（1+2i³）z=1+2i，得
$z=\frac{1+2i}{1+2{i}^{3}}=\frac{1+2i}{1-2i}=\frac{（1+2i）^{2}}{（1-2i）（1+2i）}=-\frac{3}{5}+\frac{4}{5}i$，
∴z的虚部是$\frac{4}{5}$．
故答案为：$\frac{4}{5}$．

点评本题考查复数代数形式的乘除运算，考查了复数的基本概念，是基础题．

练习册系列答案

（$\frac{1}{2}$，$\frac{1}{2}$）

D．

（$\frac{1}{3}$，$\frac{2}{3}$）

1．从1，5，9，13中的任意选一个数，4，8，12，16中任意选一个数，可构成多少个不同的分数（　　）

18．在（x²+2x+y）⁵的展开式中，x⁵y²的系数为60．

5．已知实数x，y满足x²-xy+y²=1，则x+y的最大值为（　　）

15．

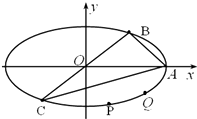如图，椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的长轴长为4，点A，B，C为椭圆上的三个点，A为椭圆的右端点，BC过中心O，且|BC|=2|AB|，S_△ABC=3．
（Ⅰ）求椭圆的标准方程；
（Ⅱ）设P，Q是椭圆上位于直线AC同侧的两个动点（异于A，C），且满足∠PBC=∠QBA，试讨论直线BP与直线BQ斜率之间的关系，并求直线PQ的斜率．

4．函数y=f（x）的图象过点P（-1，3）．则函数y=f（x）的图象关于原点O对称的图象一定过点（1，-3）．

1．求直线2x+y-6=0与直线2x+y-1=0间的距离为（　　）

2．写出命题“?x＜0，x²＞0”的否定是?x＜0，x²≤0．

试题分类