题目内容
5．已知a，b都是实数，且a＞0，b＞0，则“a＞b”是“a+lna＞b+lnb”的（ ）| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充分必要条件 | D． | 既不充分也不必要条件 |
分析 根据不等式的关系结合充分条件和必要条件的定义进行判断即可．
解答 解：当a＞0，b＞0时，若a＞b，则lna＞lnb，此时a+lna＞b+lnb成立，即充分性成立，
设f（x）=x+lnx，当x＞0时，f（x）为增函数，
则由a+lna＞b+lnb得f（a）＞f（b），即a＞b，即必要性成立，
则“a＞b”是“a+lna＞b+lnb”的充要条件，
故选：C．
点评 本题主要考查充分条件和必要条件的判断，根据不等式的性质结合函数的单调性的性质是解决本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
20．方程$\left\{\begin{array}{l}{x=sinθ}\\{y=cos2θ}\end{array}\right.$，表示的曲线上的一个点的坐标是（ ）
| A． | （2，-7） | B． | （1，0） | C． | （$\frac{1}{2}$，$\frac{1}{2}$） | D． | （$\frac{1}{3}$，$\frac{2}{3}$） |
17．某医学科研所对人体脂肪含量与年龄这两个变量研究得到一组随机样本数据，运用Excel软件计算得$\widehat{y}$=0.577x-0.448（x为人的年龄，y（单位：%）为人体脂肪含量）．对年龄为37岁的人来说，下面说法正确的是（ ）
| A． | 年龄为37岁的人体内脂肪含量都为20.90% | |
| B． | 年龄为37岁的人体内脂肪含量为21.01% | |
| C． | 年龄为37岁的人群中的大部分人的体内脂肪含量为20.90% | |
| D． | 年龄为37岁的大部分的人体内脂肪含量为31.50% |
如图，在正方体ABCD-A'B'C'D'中，E为DD'的中点．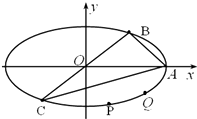
如图，椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的长轴长为4，点A，B，C为椭圆上的三个点，A为椭圆的右端点，BC过中心O，且|BC|=2|AB|，S△ABC=3．