题目内容
设函数f(x)=
cos(2x+
)+sin2x.
(1)求函数f(x)的最小正周期;
(2)若
<β<α<
,且f(
)=
,f(
)=
,求sin2α的值.
| ||
| 2 |
| π |
| 4 |
(1)求函数f(x)的最小正周期;
(2)若
| π |
| 2 |
| 3π |
| 4 |
| α-β |
| 2 |
| 4 |
| 13 |
| α+β |
| 2 |
| 4 |
| 5 |
考点:二倍角的余弦,三角函数的周期性及其求法
专题:三角函数的求值
分析:利用两角和的余弦公式以及倍角公式将已知化简为一个三角函数名称的形式,然后利用三角函数的性质解答.
解答:
解:f(x)=
cos(2x+
)+sin2x=
cos2x-
sin2x+
(1-cos2x)=
-
sin2x,
(1)函数f(x)的最小正周期T=
=π;
(2)因为f(
)=
,f(
)=
由(1)k可求sin(α-β)=
,sin(α+β)=-
.
∵
<β<α<
∴0<α-β<
π<α+β<
∴cos(α-β)=
,cos(α+β)=-
,
∴sin2α=sin[(α-β)+(α+β)]=sin(α-β)cos(α+β)+cos(α-β)sin(α+β)=-
.
| ||
| 2 |
| π |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(1)函数f(x)的最小正周期T=
| 2π |
| 2 |
(2)因为f(
| α-β |
| 2 |
| 4 |
| 13 |
| α+β |
| 2 |
| 4 |
| 5 |
由(1)k可求sin(α-β)=
| 5 |
| 13 |
| 3 |
| 5 |
∵
| π |
| 2 |
| 3π |
| 4 |
| π |
| 4 |
| 3π |
| 2 |
∴cos(α-β)=
| 12 |
| 13 |
| 4 |
| 5 |
∴sin2α=sin[(α-β)+(α+β)]=sin(α-β)cos(α+β)+cos(α-β)sin(α+β)=-
| 56 |
| 65 |
点评:本题考查了三角函数的等价变换以及角的等价变换求三角函数值;本题注意2α=(α-β)+(α+β)

练习册系列答案
相关题目
若正方形ABCD的面积为2,且
=
,
=
,
=
,则|
+
+
|等于( )
| AB |
| a |
| BC |
| b |
| AC |
| c |
| a |
| b |
| c |
| A、0 | ||
| B、2 | ||
| C、4 | ||
D、3
|
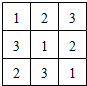 (1)如图,将1,2,3填入3×3的方格中,要求每行、每列都没有重复数字,右面是一种填法,则不同的填写方法共有几种?(用数字作答).
(1)如图,将1,2,3填入3×3的方格中,要求每行、每列都没有重复数字,右面是一种填法,则不同的填写方法共有几种?(用数字作答).