题目内容
双曲线C:
-
=1(a>0,b>0)的右焦点为F(c,0),以原点为圆心,c为半径的圆与双曲线在第二象限的交点为A,若此圆在A点处切线的斜率为
,则双曲线C的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 3 |
A、
| ||
B、
| ||
C、2
| ||
D、
|
考点:双曲线的简单性质
专题:综合题,圆锥曲线的定义、性质与方程
分析:设A(m,n),根据切线垂直于过切点的半径算出n=-
m.而以点O为圆心,c为半径的圆方程为x2+y2=c2,将A的坐标代入圆方程,算出点A的坐标,将此代入双曲线方程,并结合c2=a2+b2化简整理,再根据离心率公式整理得e4-8e2+4=0,解之即可得到该双曲线的离心率.
| 3 |
解答:
解:设A的坐标为(m,n),可得直线AO的斜率满足k=-
,即n=-
m…①
∵以点O为圆心,c为半径的圆方程为x2+y2=c2
∴将①代入圆方程,得m2+3m2=c2,解得m=-
,n=
c
将点A(-
,
c)代入双曲线方程,得
-
=1
化简得:
c2b2-
c2a2=a2b2,
∵c2=a2+b2
∴b2=c2-a2代入上式,化简整理得c4-8c2a2+4a4=0
两边都除以a4,整理得e4-8e2+4=0,解之得e2=4+2
或e2=4-2
∵双曲线的离心率e>1,∴该双曲线的离心率e=
+1(舍负).
故选:A.
| 3 |
| 3 |
∵以点O为圆心,c为半径的圆方程为x2+y2=c2
∴将①代入圆方程,得m2+3m2=c2,解得m=-
| c |
| 2 |
| ||
| 2 |
将点A(-
| c |
| 2 |
| ||
| 2 |
| ||
| a2 |
| ||
| b2 |
化简得:
| 1 |
| 4 |
| 3 |
| 4 |
∵c2=a2+b2
∴b2=c2-a2代入上式,化简整理得c4-8c2a2+4a4=0
两边都除以a4,整理得e4-8e2+4=0,解之得e2=4+2
| 3 |
| 3 |
∵双曲线的离心率e>1,∴该双曲线的离心率e=
| 3 |
故选:A.
点评:本题给出双曲线满足的条件,求双曲线的离心率,着重考查了双曲线的标准方程与简单几何性质、直线与圆的位置关系等知识,属于中档题.

练习册系列答案
相关题目
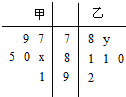 某学校从高二甲、乙两个班中各选6名同掌参加数学竞赛,他们取得的成绩(满分100分)的茎叶图如图,其中甲班学生成绩的众数是85,乙班学生成绩的平均分为81,则x+y的值为( )
某学校从高二甲、乙两个班中各选6名同掌参加数学竞赛,他们取得的成绩(满分100分)的茎叶图如图,其中甲班学生成绩的众数是85,乙班学生成绩的平均分为81,则x+y的值为( )| A、6 | B、7 | C、8 | D、9 |
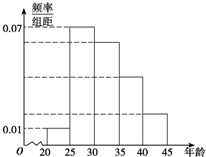 如图是依据某城市年龄在20岁到45岁的居民上网情况调查而绘制的频率分布直方图,现已知年龄在[30,35)、[35,40)、[40,45]的上网人数呈现递减的等差数列分布,则年龄在[35,40)的网民出现的频率为( )
如图是依据某城市年龄在20岁到45岁的居民上网情况调查而绘制的频率分布直方图,现已知年龄在[30,35)、[35,40)、[40,45]的上网人数呈现递减的等差数列分布,则年龄在[35,40)的网民出现的频率为( )| A、0.04 | B、0.06 |
| C、0.2 | D、0.3 |
若数列{an}的前n项和为Sn,有下列命题:
(1)若数列{an}的极限存在但不为零,则数列{Sn}的极限一定不存在;
(2)无穷数列{S2n}、{S2n-1}的极限均存在,则数列{Sn}的极限一定存在;
(3)若{an}是等差数列(公差d≠0),则S1•S2•…•Sk=O的充要条件是a1•a2•…•ak=O;
(4)若{an}是等比数列,则S1•S2•…•Sk=O(k≥2)的充要条件是an+an+1=0.
其中,错误命题的序号是( )
(1)若数列{an}的极限存在但不为零,则数列{Sn}的极限一定不存在;
(2)无穷数列{S2n}、{S2n-1}的极限均存在,则数列{Sn}的极限一定存在;
(3)若{an}是等差数列(公差d≠0),则S1•S2•…•Sk=O的充要条件是a1•a2•…•ak=O;
(4)若{an}是等比数列,则S1•S2•…•Sk=O(k≥2)的充要条件是an+an+1=0.
其中,错误命题的序号是( )
| A、(1)(2) |
| B、(2)(3) |
| C、(3)(4) |
| D、(1)(4) |
从某校高三数学学业水平测试卷中随机抽取部分试卷,对其成绩进行分析,因某特殊原因,所得的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如图,则频率分布直方图中,从左往右第四个矩形的面积为( )
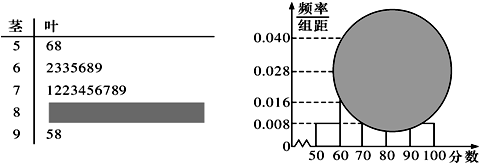

A、
| ||
B、
| ||
C、
| ||
D、
|
在等差数列{an}中,a1=-2012,其前n项和为Sn,若a12-a10=4,则S2012的值等于( )
| A、-2010 |
| B、-2011 |
| C、-2012 |
| D、-2013 |