题目内容
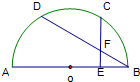如图所示，已知C，D是半圆周上的两个三等分点，直径AB=4，CE⊥AB，垂足为E，BD与CE相交于点F，则BF的长为考点：与圆有关的比例线段
专题：直线与圆
分析：连结AC，BC，由题设条件推导出∠EBF=∠CBF=∠BCF=30°，∠BEF=90°，CE=
，由此能求出BF的长．
| 3 |
解答：
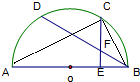解：如图，连结AC，BC，
∵C，D是半圆周上的两个三等分点，
CE⊥AB，垂足为E，BD与CE相交于点F，
∴∠ABD=∠CBD=30°，∠ACB=∠CEB=90°，
∴∠BCE=30°，∴CF=CE，
∵直径AB=4，∴CB=2，AC=
=2
，
∴CE=
AC=
，
∵∠EBF=30°，∠BEF=90°，
∴BF=CF=2EF，
∵CF+EF=CE=
，
∴BF=CF=
CE=
．
故答案为：
．
解：如图，连结AC，BC，∵C，D是半圆周上的两个三等分点，
CE⊥AB，垂足为E，BD与CE相交于点F，
∴∠ABD=∠CBD=30°，∠ACB=∠CEB=90°，
∴∠BCE=30°，∴CF=CE，
∵直径AB=4，∴CB=2，AC=
| 42-22 |
| 3 |
∴CE=
| 1 |
| 2 |
| 3 |
∵∠EBF=30°，∠BEF=90°，
∴BF=CF=2EF，
∵CF+EF=CE=
| 3 |
∴BF=CF=
| 2 |
| 3 |
2
| ||
| 3 |
故答案为：
2
| ||
| 3 |
点评：本题考查与圆有关的线段长的求法，是中档题，解题时要注意30°所对直角边等于斜边长一半这一定理的灵活运用．
练习册系列答案
相关题目
如图，设A为y轴上一点，F1，F2是椭圆的两个焦点，△AF1F2为正三角形且AF1中点B恰好在椭圆上，求此椭圆的离心率．