题目内容
已知椭圆
+
=1的左右焦点分别为F1与F2，P为椭圆上一动点，求|PF1|•|PF2|的取值范围．
| x2 |
| 16 |
| y2 |
| 15 |
考点：椭圆的简单性质
专题：圆锥曲线的定义、性质与方程
分析：由焦半径的取值范围为[a-c，a+c]，推导出3≤|PF2|≤5，由此结合椭圆的定义利用配方法能求出|PF1|•|PF2|的取值范围．
解答：
解：椭圆
+
=1中，
a=4，b=
，c=1，
∵焦半径的取值范围为[a-c，a+c]，
∴3≤|PF2|≤5，
∵|PF1|•|PF2|=（8-|PF2|）|PF2|=-（|PF2|-4）2+16，
∵-1≤|PF2|-4≤1，
∴15≤|PF1|•|PF2|≤16，
∴|PF1|•|PF2|的取值范围是[15，16]．
| x2 |
| 16 |
| y2 |
| 15 |
a=4，b=
| 15 |
∵焦半径的取值范围为[a-c，a+c]，
∴3≤|PF2|≤5，
∵|PF1|•|PF2|=（8-|PF2|）|PF2|=-（|PF2|-4）2+16，
∵-1≤|PF2|-4≤1，
∴15≤|PF1|•|PF2|≤16，
∴|PF1|•|PF2|的取值范围是[15，16]．
点评：本题考查椭圆上焦半径乘积的取值范围，是中档题，解题时要认真审题，注意配方法的合理运用．
练习册系列答案
优生乐园系列答案
新编小学单元自测题系列答案
相关题目
某地为发展旅游业，在旅游手册中给出了当地一年12个月每个月的平均气温如图所示（气温单位：℃）．根据图中提供的数据，试用y=Asin（ωt+φ）+b近似地拟合出月平均气温与时间（单位：月）的函数关系，并求出其周期和振幅、气温达到最大值与最小值的时间．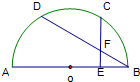
如图所示，已知C，D是半圆周上的两个三等分点，直径AB=4，CE⊥AB，垂足为E，BD与CE相交于点F，则BF的长为