题目内容
设集合A={x|x2+bx+c=x},B={x|(x-1)2+b(x-1)+c=x+1},若A={2},求集合B.
考点:集合的表示法
专题:集合
分析:根据集合A={2},求出b,c的值,然后即可得到集合B的元素.
解答:
解:A={x|x2+bx+c=x}={x|x2+(b-1)x+c=0},
∵A={2},
∴根据根与系数之间的关系的
,
即
,
∴B={x|(x-1)2+b(x-1)+c=x+1}={x|(x-1)2-3(x-1)+4=x+1}={x|x2-6x+3=0}={3+
,3-
},
∵A={2},
∴根据根与系数之间的关系的
|
即
|
∴B={x|(x-1)2+b(x-1)+c=x+1}={x|(x-1)2-3(x-1)+4=x+1}={x|x2-6x+3=0}={3+
| 6 |
| 6 |
点评:本题主要考查集合元素的求法,以及集合的表示,比较基础.

练习册系列答案
 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案
相关题目
已知m和2n的等差中项是4,2m和n的等差中项是5,则m和n的等差中项是( )
| A、2 | B、3 | C、6 | D、9 |
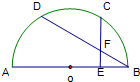 如图所示,已知C,D是半圆周上的两个三等分点,直径AB=4,CE⊥AB,垂足为E,BD与CE相交于点F,则BF的长为
如图所示,已知C,D是半圆周上的两个三等分点,直径AB=4,CE⊥AB,垂足为E,BD与CE相交于点F,则BF的长为