题目内容
已知函数f(x)=x2,g(x)=2lnx.
(Ⅰ)设h(x)=f(x)-g(x),求h(x)的最小值;
(Ⅱ)如何上下平移f(x)的图象,使得f(x)平移后的图象与g(x)的图象有公共点且在公共点处切线相同.
(Ⅰ)设h(x)=f(x)-g(x),求h(x)的最小值;
(Ⅱ)如何上下平移f(x)的图象,使得f(x)平移后的图象与g(x)的图象有公共点且在公共点处切线相同.
考点:利用导数求闭区间上函数的最值,利用导数研究曲线上某点切线方程
专题:综合题,导数的综合应用
分析:(Ⅰ)表示出h(x),利用导数求出极值,可判断即为最小值;
(Ⅱ)设上下平移f(x)的图象为c个单位的函数解析式为y=x2+c.设y=x2+c与y=2lnx的公共点为(x0,y0).依题意有:
,解出可得.
(Ⅱ)设上下平移f(x)的图象为c个单位的函数解析式为y=x2+c.设y=x2+c与y=2lnx的公共点为(x0,y0).依题意有:
|
解答:
解:(Ⅰ)h(x)=x2-2lnx,则h'(x)=2x-
,
令h'(x)=0,解得x=1,
当x∈(0,1)时,h'(x)<0,h(x)递减;当x∈(1,+∞)时,h'(x)>0,h(x)递增;
∴当x=1时,h(x)达到最小,h(x)的最小值为h(1)=1.
(Ⅱ)设上下平移f(x)的图象为c个单位的函数解析式为y=x2+c.
设y=x2+c与y=2lnx的公共点为(x0,y0).
依题意有:
,
解得x0=1,c=-1,
故将f(x)的图象向下平移1个单位后,两函数图象在公共点(1,0)处有相同的切线.
| 2 |
| x |
令h'(x)=0,解得x=1,
当x∈(0,1)时,h'(x)<0,h(x)递减;当x∈(1,+∞)时,h'(x)>0,h(x)递增;
∴当x=1时,h(x)达到最小,h(x)的最小值为h(1)=1.
(Ⅱ)设上下平移f(x)的图象为c个单位的函数解析式为y=x2+c.
设y=x2+c与y=2lnx的公共点为(x0,y0).
依题意有:
|
解得x0=1,c=-1,
故将f(x)的图象向下平移1个单位后,两函数图象在公共点(1,0)处有相同的切线.
点评:本题考查利用导数求函数的最值、导数的几何意义、图象的平移变换,属中档题,正确理解导数与函数最值的关系是解题基础.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案
相关题目
 某地为发展旅游业,在旅游手册中给出了当地一年12个月每个月的平均气温如图所示(气温单位:℃).根据图中提供的数据,试用y=Asin(ωt+φ)+b近似地拟合出月平均气温与时间(单位:月)的函数关系,并求出其周期和振幅、气温达到最大值与最小值的时间.
某地为发展旅游业,在旅游手册中给出了当地一年12个月每个月的平均气温如图所示(气温单位:℃).根据图中提供的数据,试用y=Asin(ωt+φ)+b近似地拟合出月平均气温与时间(单位:月)的函数关系,并求出其周期和振幅、气温达到最大值与最小值的时间.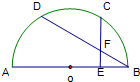 如图所示,已知C,D是半圆周上的两个三等分点,直径AB=4,CE⊥AB,垂足为E,BD与CE相交于点F,则BF的长为
如图所示,已知C,D是半圆周上的两个三等分点,直径AB=4,CE⊥AB,垂足为E,BD与CE相交于点F,则BF的长为