题目内容
 如图,设A为y轴上一点,F1,F2是椭圆的两个焦点,△AF1F2为正三角形且AF1中点B恰好在椭圆上,求此椭圆的离心率.
如图,设A为y轴上一点,F1,F2是椭圆的两个焦点,△AF1F2为正三角形且AF1中点B恰好在椭圆上,求此椭圆的离心率.考点:椭圆的简单性质
专题:圆锥曲线的定义、性质与方程
分析:由已知条件,推导出|BF1|=c,|BF2|=
c,由椭圆定义知:|BF1|+|BF2|=2a,由此有求出结果.
| 3 |
解答:
解:∵F1,F2是椭圆的两个焦点,
△AF1F2为正三角形且AF1中点B恰好在椭圆上,
∴|BF1|=
|F1F2|=c,且∠F1BF2 =90°,
∴|BF2|=
=
c,
由椭圆定义知:|BF1|+|BF2|=2a,
即c+
c=2a,
∴c=
a=(
-1)a,
∴e=
=
-1.

△AF1F2为正三角形且AF1中点B恰好在椭圆上,
∴|BF1|=
| 1 |
| 2 |
∴|BF2|=
| (2c)2-c2 |
| 3 |
由椭圆定义知:|BF1|+|BF2|=2a,
即c+
| 3 |
∴c=
| 2 | ||
|
| 3 |
∴e=
| c |
| a |
| 3 |
点评:本题考查椭圆的离心率的求法,是中档题,解题时要认真审题,注意椭圆性质的灵活运用.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
cos57°cos12°+sin57°sin12°=( )
A、
| ||||
| B、0 | ||||
C、
| ||||
D、
|
已知m和2n的等差中项是4,2m和n的等差中项是5,则m和n的等差中项是( )
| A、2 | B、3 | C、6 | D、9 |
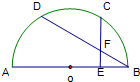 如图所示,已知C,D是半圆周上的两个三等分点,直径AB=4,CE⊥AB,垂足为E,BD与CE相交于点F,则BF的长为
如图所示,已知C,D是半圆周上的两个三等分点,直径AB=4,CE⊥AB,垂足为E,BD与CE相交于点F,则BF的长为