题目内容
f(x)=x2-2x+5的定义域为A,值域为B,则集合A与B的关系是 .
考点:函数的定义域及其求法
专题:函数的性质及应用
分析:根据二次函数的性质求出函数的定义域和值域即可得到结论.
解答:
解:要使函数有意义,则x∈R,
f(x)=x2-2x+5=(x-1)2+4≥4,
即函数的定义域为A=R,值域B=[4,+∞),
∴B?A,
故答案为:B?A
f(x)=x2-2x+5=(x-1)2+4≥4,
即函数的定义域为A=R,值域B=[4,+∞),
∴B?A,
故答案为:B?A
点评:本题主要考查函数定义域和值域的求法以及集合关系的判断,比较基础.

练习册系列答案
相关题目
将一张画了直角坐标系(两坐标轴单位长度相同)的纸折叠一次,使点(2,0)与点(-2,4)重合,则与点(5,8)重合的点是( )
| A、(6,7) |
| B、(7,6) |
| C、(-5,-4) |
| D、(-4,-5) |
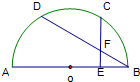 如图所示,已知C,D是半圆周上的两个三等分点,直径AB=4,CE⊥AB,垂足为E,BD与CE相交于点F,则BF的长为
如图所示,已知C,D是半圆周上的两个三等分点,直径AB=4,CE⊥AB,垂足为E,BD与CE相交于点F,则BF的长为