题目内容
5.已知向量$\overrightarrow{a}$=(1,2),$\overrightarrow{a}$⊥$\overrightarrow{b}$,则$\overrightarrow{b}$可以为( )| A. | (1,2) | B. | (1,-2) | C. | (2,1) | D. | (2,-1) |
分析 设$\overrightarrow{b}$=(m,n),运用向量垂直的条件:数量积为0,可得m+2n=0,代入选项即可得到所求.
解答 解:设$\overrightarrow{b}$=(m,n),
由$\overrightarrow{a}$=(1,2),$\overrightarrow{a}$⊥$\overrightarrow{b}$,
可得$\overrightarrow{a}$•$\overrightarrow{b}$=0,
即有m+2n=0,
对照选项,可得选项D,代入可得
2+2×(-1)=0.
故选D.
点评 本题考查向量垂直的条件:数量积为0,考查运算能力,属于基础题.

练习册系列答案
相关题目
16.设等差数列{an}的前n项和为Sn,已知S3=5,S6=15,则S9=( )
| A. | 35 | B. | 30 | C. | 25 | D. | 15 |
13.若函数y=x2-x的图象在点x=2处的切线被圆C:x2+y2=r2(r>0)所截得的弦长是$\frac{2\sqrt{10}}{5}$,则r=( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | 1 | C. | $\sqrt{2}$ | D. | 2 |
20.已知过点A(0,0)和B(4,m)的直线与直线2x-y-1=0平行,则m的值为( )
| A. | -8 | B. | -2 | C. | 2 | D. | 8 |
10.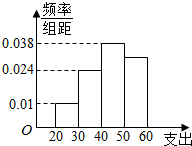 学校为了调查学生在课外读物方面的支出情况,抽出了一个容量为n且支出在[20,60)元的样本,其频率分布直方图如图所示,其中支出在[50,60)元的学生有30人,则n的值为( )
学校为了调查学生在课外读物方面的支出情况,抽出了一个容量为n且支出在[20,60)元的样本,其频率分布直方图如图所示,其中支出在[50,60)元的学生有30人,则n的值为( )
 学校为了调查学生在课外读物方面的支出情况,抽出了一个容量为n且支出在[20,60)元的样本,其频率分布直方图如图所示,其中支出在[50,60)元的学生有30人,则n的值为( )
学校为了调查学生在课外读物方面的支出情况,抽出了一个容量为n且支出在[20,60)元的样本,其频率分布直方图如图所示,其中支出在[50,60)元的学生有30人,则n的值为( )| A. | 100 | B. | 1000 | C. | 90 | D. | 900 |
17.在平面直角坐标系中,A,B分别是x轴和y轴上的动点,若以AB为直径的圆C与直线3x+y-4=0相切,则圆C面积的最小值为( )
| A. | $\frac{5π}{4}$ | B. | $\frac{2π}{5}$ | C. | $(6-2\sqrt{5})π$ | D. | $\frac{5π}{2}$ |