Question

19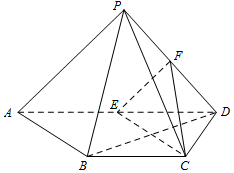．如图，四棱锥P-ABCD中，PD⊥平面PAB，AD∥BC，BC=CD=$\frac{1}{2}$AD，E，F分别为线段AD，PD的中点．
（Ⅰ）求证：CE∥平面PAB；
（Ⅱ）求证：PD⊥平面CEF；
（Ⅲ）写出三棱锥D-CEF与三棱锥P-ABD的体积之比．（结论不要求证明）

Answer 1

分析 （Ⅰ）推导出四边形ABCE为平行四边形，从而CE∥AB，由此能证明CE∥平面PAB．
（Ⅱ）推导出EF∥PA，则PD⊥AB，PD⊥PA，从而PD⊥EF，由CE∥AB，得PD⊥CE，由此能证明PD⊥平面CEF．
（Ⅲ）由三棱锥的体积公式能求出三棱锥D-CEF与三棱锥P-ABD的体积之比．

解答 证明：（Ⅰ）∵BC∥AD，BC=$\frac{1}{2}AD$，E为AD中点，
∴AE∥BC，且AE=BC，
∴四边形ABCE为平行四边形，
∴CE∥AB，
又AB?平面PAB，CE?平面PAB，
∴CE∥平面PAB．
（Ⅱ）∵E、F分别为AD、PD的中点，∴EF∥PA，
又∵PD⊥平面PAB，PA，AB?平面PAB，
∴PD⊥AB，PD⊥PA，∴PD⊥EF，
又CE∥AB，∴PD⊥CE，
∵EF∩CE=E，
∴PD⊥平面CEF．
解：（Ⅲ）三棱锥D-CEF与三棱锥P-ABD的体积之比为：
$\frac{{V}_{D-CEF}}{{V}_{P-ABD}}$=$\frac{1}{4}$．

点评 本题考查线面平行、线面垂直的证明，考查两个三棱锥的体积之比的求法，考查空间中线线、线面、面面间的位置关系等基础知识，考查推理论证能力、运算求解能力，考查化归与转化思想、数形结合思想，是中档题．