题目内容
7.已知函数f (x)的定义域为R.当x<0时,f(x)=ln(-x)+x;当-e≤x≤e时,f(-x)=-f(x);当x>1时,f(x+2)=f(x),则f(8)=2-ln2.分析 求得函数的周期为2,再利用当-e≤x≤e时,f(-x)=-f(x),得到f(2)=-f(-2),当x<0时,f(x)=ln(-x)+x,得到f(-2)=ln2-2,即可得出结论.
解答 解:∵当x>1时,f(x+2)=f(x),
∴当x>1时,f(x)的周期为2.
∴f(8)=f(2),
∵当-e≤x≤e时,f(-x)=-f(x),
∴f(2)=-f(-2),
∵当x<0时,f(x)=ln(-x)+x,
∴f(-2)=ln2-2,
∴f(8)=f(2)=2-ln2,
故答案为:2-ln2.
点评 本题考查函数值的计算,考查函数的周期性,考查学生的计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.某市对大学生毕业后自主创业人员给予小额贷款补贴,贷款期限分为6个月、12个月、18个月、24个月、36个月五种,对于这五种期限的贷款政府分别补贴200元、300元、300元、400元、400元,从2016年享受此项政策的自主创业人员中抽取了100人进行调查统计,选取贷款期限的频数如表:
以上表中各种贷款期限的频数作为2017年自主创业人员选择各种贷款期限的概率.
(Ⅰ)某大学2017年毕业生中共有3人准备申报此项贷款,计算其中恰有两人选择贷款期限为12个月的概率;
(Ⅱ)设给某享受此项政策的自主创业人员补贴为X元,写出X的分布列;该市政府要做预算,若预计2017年全市有600人申报此项贷款,则估计2017年该市共要补贴多少万元.
| 贷款期限 | 6个月 | 12个月 | 18个月 | 24个月 | 36个月 |
| 频数 | 20 | 40 | 20 | 10 | 10 |
(Ⅰ)某大学2017年毕业生中共有3人准备申报此项贷款,计算其中恰有两人选择贷款期限为12个月的概率;
(Ⅱ)设给某享受此项政策的自主创业人员补贴为X元,写出X的分布列;该市政府要做预算,若预计2017年全市有600人申报此项贷款,则估计2017年该市共要补贴多少万元.
15.某翻译公司为提升员工业务能力,为员工开设了英语、法语、西班牙语和德语四个语种的培训过程,要求每名员工参加且只参加其中两种.无论如何安排,都有至少5名员工参加的培训完全相同.问该公司至少有多少名员工?( )
| A. | 17 | B. | 21 | C. | 25 | D. | 29 |
2.下列函数中,既是偶函数又是(0,+∞)上的增函数的是( )
| A. | y=-x3 | B. | y=2|x| | C. | y=${x}^{\frac{1}{2}}$ | D. | y=log3(-x) |
12.圆(x+1)2+y2=1的圆心到直线y=x-1的距离为( )
| A. | 1 | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\sqrt{2}$ | D. | 2 |
16.某电子产品公司前四年的年宣传费x(单位:千万元)与年销售量y(单位:百万部)的数据如下表所示:
可以求y关于x的线性回归方程为$\stackrel{∧}{y}$=1.9x+1.
(1)该公司下一年准备投入10千万元的宣传费,根据所求得的回归方程预测下一年的销售量m:
(2)根据下表所示五个散点数据,求出y关于x的线性回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$.
并利用小二乘法的原理说明$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$与$\stackrel{∧}{y}$=1.9x+1的关系.
参考公式:回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$中斜率和截距的最小二乘法估计公式分别为:
$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{{\sum_{i=1}^{n}x}_{i}^{2}-n{\overline{x}}^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$.
| x(单位:千万元) | 1 | 2 | 3 | 4 |
| y(单位:百万部) | 3 | 5 | 6 | 9 |
(1)该公司下一年准备投入10千万元的宣传费,根据所求得的回归方程预测下一年的销售量m:
(2)根据下表所示五个散点数据,求出y关于x的线性回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$.
| x(单位:千万元) | 1 | 2 | 3 | 4 | 10 |
| y(单位:百万部) | 3 | 5 | 6 | 9 | m |
参考公式:回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$中斜率和截距的最小二乘法估计公式分别为:
$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{{\sum_{i=1}^{n}x}_{i}^{2}-n{\overline{x}}^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$.
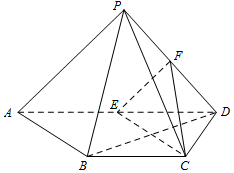 如图,四棱锥P-ABCD中,PD⊥平面PAB,AD∥BC,BC=CD=$\frac{1}{2}$AD,E,F分别为线段AD,PD的中点.
如图,四棱锥P-ABCD中,PD⊥平面PAB,AD∥BC,BC=CD=$\frac{1}{2}$AD,E,F分别为线段AD,PD的中点.