题目内容
4.一个袋中装有1红,2白和2黑共5个小球,这5个小球除颜色外其它都相同,现从袋中任取2个球,则至少取到1个白球的概率为$\frac{7}{10}$.分析 记1个红球为A,2个白球为B1,B2,2个黑球为C1,C2,从中任取2个,利用列举法能求出至少取到1个白球的概率.
解答 解:记1个红球为A,2个白球为B1,B2,
2个黑球为C1,C2,
从中任取2个的基本事件有10个,分别为:
(A,B1),(A,B2),(A,C1),(A,C2),(B1,B2),
(B1,C1),(B1,C2),(B2,C1),(B2,C2),(C1,C2),
其中至少取到1个白球的基本事件有7个,
故至少取到1个白球的概率为:p=$\frac{7}{10}$.
故答案为:$\frac{7}{10}$.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意列举法的合理运用.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
15.某翻译公司为提升员工业务能力,为员工开设了英语、法语、西班牙语和德语四个语种的培训过程,要求每名员工参加且只参加其中两种.无论如何安排,都有至少5名员工参加的培训完全相同.问该公司至少有多少名员工?( )
| A. | 17 | B. | 21 | C. | 25 | D. | 29 |
12.圆(x+1)2+y2=1的圆心到直线y=x-1的距离为( )
| A. | 1 | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\sqrt{2}$ | D. | 2 |
9.牛顿法求方程f(x)=0近似根原理如下:求函数y=f(x)在点(xn,f(xn))处的切线y=f′(xn)(x-xn)+f(xn),其与x轴交点横坐标xn+1=xn-$\frac{f({x}_{n})}{f′({x}_{n})}$(n∈N*),则xn+1比xn更靠近f(x)=0的根,现已知f(x)=x2-3,求f(x)=0的一个根的程序框图如图所示,则输出的结果为( )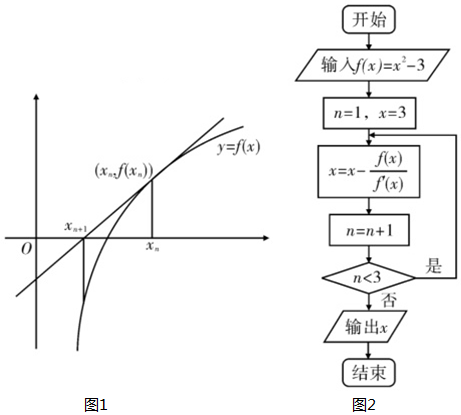

| A. | 2 | B. | 1.75 | C. | 1.732 | D. | 1.73 |
16.某电子产品公司前四年的年宣传费x(单位:千万元)与年销售量y(单位:百万部)的数据如下表所示:
可以求y关于x的线性回归方程为$\stackrel{∧}{y}$=1.9x+1.
(1)该公司下一年准备投入10千万元的宣传费,根据所求得的回归方程预测下一年的销售量m:
(2)根据下表所示五个散点数据,求出y关于x的线性回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$.
并利用小二乘法的原理说明$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$与$\stackrel{∧}{y}$=1.9x+1的关系.
参考公式:回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$中斜率和截距的最小二乘法估计公式分别为:
$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{{\sum_{i=1}^{n}x}_{i}^{2}-n{\overline{x}}^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$.
| x(单位:千万元) | 1 | 2 | 3 | 4 |
| y(单位:百万部) | 3 | 5 | 6 | 9 |
(1)该公司下一年准备投入10千万元的宣传费,根据所求得的回归方程预测下一年的销售量m:
(2)根据下表所示五个散点数据,求出y关于x的线性回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$.
| x(单位:千万元) | 1 | 2 | 3 | 4 | 10 |
| y(单位:百万部) | 3 | 5 | 6 | 9 | m |
参考公式:回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$中斜率和截距的最小二乘法估计公式分别为:
$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{{\sum_{i=1}^{n}x}_{i}^{2}-n{\overline{x}}^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$.
 如图,椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率为$e=\frac{{\sqrt{3}}}{2}$,顶点为A1、A2、B1、B2,且$\overrightarrow{{A_1}{B_1}}•\overrightarrow{{A_1}{B_2}}=3$.
如图,椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率为$e=\frac{{\sqrt{3}}}{2}$,顶点为A1、A2、B1、B2,且$\overrightarrow{{A_1}{B_1}}•\overrightarrow{{A_1}{B_2}}=3$.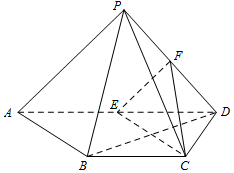 如图,四棱锥P-ABCD中,PD⊥平面PAB,AD∥BC,BC=CD=$\frac{1}{2}$AD,E,F分别为线段AD,PD的中点.
如图,四棱锥P-ABCD中,PD⊥平面PAB,AD∥BC,BC=CD=$\frac{1}{2}$AD,E,F分别为线段AD,PD的中点.