题目内容
14.在△ABC中,角A,B,C对应的边长分别是a,b,c,且$\sqrt{3}asinB=bcosA$,则角A的大小为 $\frac{π}{6}$.分析 由已知及正弦定理可解得tanA的值,从而可求A的值;
解答 解:∵$\sqrt{3}$asinB=bcosA.
∴$\frac{a}{\frac{cosA}{\sqrt{3}}}$=$\frac{b}{sinB}$,
又由正弦定理知:$\frac{a}{sinA}=\frac{b}{sinB}$
∴可得sinA=$\frac{cosA}{\sqrt{3}}$,从而可解得tanA=$\frac{\sqrt{3}}{3}$,
∵0<A<π,
∴A=$\frac{π}{6}$.
故答案为:$\frac{π}{6}$.
点评 本题主要考察了正弦定理、余弦定理的综合应用,属于基本知识的考查.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
2.下列函数中,既是偶函数又是(0,+∞)上的增函数的是( )
| A. | y=-x3 | B. | y=2|x| | C. | y=${x}^{\frac{1}{2}}$ | D. | y=log3(-x) |
6.在复平面内,复数z的对应点为(1,2),复数z的共轭复数为( )
| A. | 1+2i | B. | 1-2i | C. | -2+i | D. | -2-i |
4.已知实数a,b满足(a+2i)•bi=3i+6(i为虚数单位)则在复平面内,复数z=a+bi所对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
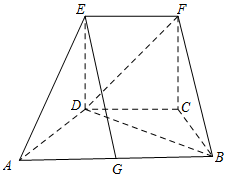 如图所示的几何体中,四边形ABCD为等腰梯形,AB∥CD,AB=2AD=2,∠DAB=60°,四边形CDEF为正方形,平面CDEF⊥平面ABCD.
如图所示的几何体中,四边形ABCD为等腰梯形,AB∥CD,AB=2AD=2,∠DAB=60°,四边形CDEF为正方形,平面CDEF⊥平面ABCD.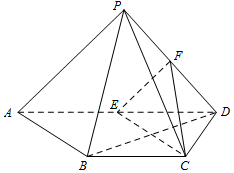 如图,四棱锥P-ABCD中,PD⊥平面PAB,AD∥BC,BC=CD=$\frac{1}{2}$AD,E,F分别为线段AD,PD的中点.
如图,四棱锥P-ABCD中,PD⊥平面PAB,AD∥BC,BC=CD=$\frac{1}{2}$AD,E,F分别为线段AD,PD的中点.