题目内容
17．$k=±\frac{{\sqrt{5}}}{2}$是直线y=kx-1与曲线x2-y2=4仅有一个公共点的（ ）| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分又不必要条件 |
分析 把直线y=kx-1方程代入曲线x2-y2=4，化为：（k2-1）x2-2kx+5=0，由△=0，解得k=$±\frac{\sqrt{5}}{2}$．此时直线与双曲线有唯一公共点．当k=±1时，直线y=kx-1与曲线x2-y2=4仅有一个公共点．j即可判断出结论．
解答 解：把直线y=kx-1方程代入曲线x2-y2=4，化为：（k2-1）x2-2kx+5=0，由△=4k2-20（k2-1）=0，解得k=$±\frac{\sqrt{5}}{2}$．此时直线与双曲线有唯一公共点．
当k=±1时，直线y=kx-1与曲线x2-y2=4仅有一个公共点．
∴$k=±\frac{{\sqrt{5}}}{2}$是直线y=kx-1与曲线x2-y2=4仅有一个公共点的充分不必要条件．
故选：A．
点评 本题考查了直线与双曲线的交点与判别式的关系、简易逻辑的判定方法，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
8．已知方程$\frac{x^2}{2-k}+\frac{y^2}{2k+1}=1$表示焦点在y轴上的椭圆，则实数k的取值范围是（ ）
| A． | $（\frac{1}{2}，2）$ | B． | （2，+∞） | C． | （1，2） | D． | $（\frac{1}{2}，1）$ |
5．已知i是虚数单位，复数z=m-1+（m+1）i，（其中m∈R）是纯虚数，则m=（ ）
| A． | -1 | B． | 1 | C． | ±1 | D． | 0 |
12．已知${（{1+x}）^{10}}={a_0}+{a_1}（{1-x}）+{a_2}{（{1-x}）^2}+L+{a_{10}}{（{1-x}）^{10}}$，则a8等于（ ）
| A． | -5 | B． | 5 | C． | 90 | D． | 180 |
2．已知函数f（x）=ex-e-x+4sin3x+1，x∈（-1，1），若f（1-a）+f（1-a2）＞2成立，则实数a的取值范围是（ ）
| A． | （-2，1） | B． | （0，1） | C． | $（{1，\sqrt{2}}）$ | D． | （-∞，-2）∪（1，+∞） |
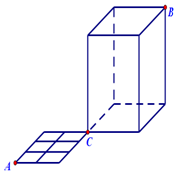如图，一只蚂蚁从点A出发沿着水平面的线条爬行到点C，再由点C沿着置于水平面的长方体的棱爬行至顶点B，则它可以爬行的不同的最短路径有（ ）条．