题目内容
11.点P在曲线$\frac{x^2}{2}-{y^2}$=1上,点Q在曲线x2+(y-3)2=4上,线段PQ的中点为M,O是坐标原点,则线段OM长的最小值是$\sqrt{2}$-1.分析 设设Q(x1,y1),P(x2,y2),P1(-x2,-y2),则|OM|=$\frac{1}{2}$|P1Q|,求出P1到圆心N(0,3)的最小距离,即可得出|P1Q|的最小距离,从而得出|OM|的最小值.
解答  解:设Q(x1,y1),P(x2,y2),则M($\frac{{x}_{1}+{x}_{2}}{2}$,$\frac{{y}_{1}+{y}_{2}}{2}$),
解:设Q(x1,y1),P(x2,y2),则M($\frac{{x}_{1}+{x}_{2}}{2}$,$\frac{{y}_{1}+{y}_{2}}{2}$),
∴|OM|=$\frac{1}{2}$$\sqrt{({x}_{1}+{x}_{2})^{2}+({y}_{1}+{y}_{2})^{2}}$,
设P1(-x2,-y2),则P1在双曲线上,∴x12=2y22+11,
∴|P1Q|=$\sqrt{({x}_{1}+{x}_{2})^{2}+({y}_{1}+{y}_{2})^{2}}$,|OM|=$\frac{1}{2}$|P1Q|.
设曲线x2+(y-3)2=4的圆心为N(0,3),
则|P1Q|min=|P1N|min-2,
∵|P1N|=$\sqrt{{{x}_{2}}^{2}+(3+{y}_{2})^{2}}$=$\sqrt{3{{y}_{2}}^{2}+6{y}_{2}+11}$=$\sqrt{3({y}_{2}+1)^{2}+8}$,
∴当y2=-1时,|P1N|min=2$\sqrt{2}$,
∴|P1Q|min=2$\sqrt{2}$-2,
∴|OM|min=$\sqrt{2}-1$.
故答案为:$\sqrt{2}-1$.
点评 本题考查了双曲线的性质,距离公式的应用,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.下列各组函数f(x)与g(x)相同的是( )
| A. | f(x)=1,g(x)=x0 | B. | f(x)=x2,g(x)=(x+1)2 | ||
| C. | f(x)=x,g(x)=elnx | D. | f(x)=|x|,g(x)=$\left\{\begin{array}{l}{x,}&{x≥0}\\{-x,}&{x<0}\end{array}\right.$ |
1.若复数$\frac{a+i}{1+2i}({a∈R})$为纯虚数,其中i为虚数单位,则a=( )
| A. | 2 | B. | $\frac{1}{2}$ | C. | -2 | D. | $-\frac{1}{2}$ |
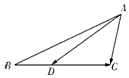 如图,在△ABC中,∠BAC=60°,AB=2,AC=1,D是BC边上一点,且$\overrightarrow{CD}$=2$\overrightarrow{DB}$,则$\overrightarrow{AD}$•$\overrightarrow{BC}$ 的值为-2.
如图,在△ABC中,∠BAC=60°,AB=2,AC=1,D是BC边上一点,且$\overrightarrow{CD}$=2$\overrightarrow{DB}$,则$\overrightarrow{AD}$•$\overrightarrow{BC}$ 的值为-2.