题目内容
 已知椭圆C:
已知椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
2
| ||
| 3 |
(1)求椭圆C的方程;
(2)设过点A的直线与C相交于P、Q两点,当△OPQ的面积最大时,求l的方程.
考点:直线与圆锥曲线的综合问题,椭圆的标准方程
专题:圆锥曲线的定义、性质与方程
分析:(1)利用椭圆的离心率以及直线的斜率,求出椭圆的几何量,然后求椭圆C的方程;
(2)由设直线的斜率为k,方程为y=kx-2,联立直线与椭圆方程,通过△=16(4k2-3)>0,求出k的范围,设P(x1,y1),Q(x2,y2),利用韦达定理,求出|PQ|,坐标原点O到直线的距离,得到S△OPQ的表达式,利用换元法以及基本不等式,通过面积的最大值,求出k的值,得到直线方程.
(2)由设直线的斜率为k,方程为y=kx-2,联立直线与椭圆方程,通过△=16(4k2-3)>0,求出k的范围,设P(x1,y1),Q(x2,y2),利用韦达定理,求出|PQ|,坐标原点O到直线的距离,得到S△OPQ的表达式,利用换元法以及基本不等式,通过面积的最大值,求出k的值,得到直线方程.
解答:
解:(1)设F(c,0),由题意kAF=
=
,
∴e=
,又∵离心率
=
,∴a=2,
∴b=
=1,椭圆C的方程为
+y2=1;-----------------------(4分)
(2)由题意知,直线的斜率存在,设直线的斜率为k,方程为y=kx-2,
联立直线与椭圆方程:
,化简得:(1+4k2)x2-16kx+12=0,
由△=16(4k2-3)>0,∴k2>
,
设P(x1,y1),Q(x2,y2),则 x1+x2=
,x1x2=
,--------------------(6分)
∴|PQ|=
|x1-x2|=
•
,
坐标原点O到直线的距离为d=
,
S△OPQ=
•
•
=
,-----------------(8分)
令t=
(t>0),则 S△OPQ=
=
,
∵t+
≥4,当且仅当t=
,即t=2时等号成立,
∴S△OPQ≤1,故当t=2,即
=2,k2=
>
,
∴k=±
时,△OPQ的面积最大,------------------------(10分)
此时直线的方程为:y=±
x-2.---------------------(12分)
| 2 |
| c |
2
| ||
| 3 |
∴e=
| 3 |
| c |
| a |
| ||
| 2 |
∴b=
| a2-c2 |
| x2 |
| 4 |
(2)由题意知,直线的斜率存在,设直线的斜率为k,方程为y=kx-2,
联立直线与椭圆方程:
|
由△=16(4k2-3)>0,∴k2>
| 3 |
| 4 |
设P(x1,y1),Q(x2,y2),则 x1+x2=
| 16k |
| 1+4k2 |
| 12 |
| 1+4k2 |
∴|PQ|=
| 1+k2 |
| 1+k2 |
4
| ||
| 1+4k2 |
坐标原点O到直线的距离为d=
| 2 | ||
|
S△OPQ=
| 1 |
| 2 |
| 1+k2 |
4
| ||
| 1+4k2 |
| 2 | ||
|
4
| ||
| 1+4k2 |
令t=
| 4k2-3 |
| 4t |
| t2+4 |
| 4 | ||
t+
|
∵t+
| 4 |
| t |
| 4 |
| t |
∴S△OPQ≤1,故当t=2,即
| 4k2-3 |
| 7 |
| 4 |
| 3 |
| 4 |
∴k=±
| ||
| 2 |
此时直线的方程为:y=±
| ||
| 2 |
点评:本题考查椭圆的方程的求法,直线与椭圆的方程的综合应用,考查分析问题解决问题的能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
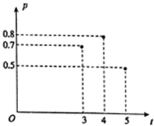 加工爆米花时,爆开且不糊的粒数占加工总粒数的百分比称为“可食用率”,在特定条件下,可食用率p与加工时间t(单位:分钟)满足下列某函数关系:①p=at+b②p=alogbt③p=at2+bt+c(a,b,c是常数),如图记录了三次实验的数据,
加工爆米花时,爆开且不糊的粒数占加工总粒数的百分比称为“可食用率”,在特定条件下,可食用率p与加工时间t(单位:分钟)满足下列某函数关系:①p=at+b②p=alogbt③p=at2+bt+c(a,b,c是常数),如图记录了三次实验的数据,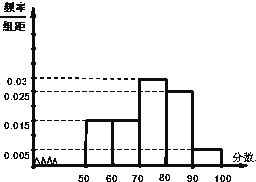 高二年级从参加期末考试的学生中抽出60名学生,并统计了他们的物理成绩(成绩均为整数且满分为100分),把其中不低于50分的分成五段[50,60),[60,70)…[90,100]后画出如下部分频率分布直方图.观察图形的信息,回答下列问题:
高二年级从参加期末考试的学生中抽出60名学生,并统计了他们的物理成绩(成绩均为整数且满分为100分),把其中不低于50分的分成五段[50,60),[60,70)…[90,100]后画出如下部分频率分布直方图.观察图形的信息,回答下列问题: