题目内容
已知函数f(x)=ax-
,且f(-2)=-
.
(1)求f(x)的解析式;
(2)判断函数f(x)在(0,+∞)上的单调性并加以证明;
(3)求函数f(x)在[
,2]上的最大值和最小值.
| 1 |
| x |
| 3 |
| 2 |
(1)求f(x)的解析式;
(2)判断函数f(x)在(0,+∞)上的单调性并加以证明;
(3)求函数f(x)在[
| 1 |
| 2 |
考点:函数的最值及其几何意义,函数解析式的求解及常用方法,函数单调性的判断与证明
专题:综合题,函数的性质及应用
分析:(1)利用函数f(x)=ax-
,且f(-2)=-
,求出a,即可求f(x)的解析式;
(2)f(x)在(0,+∞)上是增函数,利用单调性的定义加以证明;
(3)f(x)在[
,2]上是增函数,可求函数f(x)在[
,2]上的最大值和最小值.
| 1 |
| x |
| 3 |
| 2 |
(2)f(x)在(0,+∞)上是增函数,利用单调性的定义加以证明;
(3)f(x)在[
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:(1)∵f(-2)=-
,
∴-2a+
=-
…(1分)
得a=1,∴f(x)=x-
…(3分)
(2)f(x)在(0,+∞)上是增函数
设x1,x2∈(0,+∞),且x1<x2…(4分)
f(x1)-f(x2)=x1-
-x2+
=
…(7分)
∵0<x1<x2
∴x1-x2<0,x1x2>0,x1x2+1>0…(8分)
∴f(x1)-f(x2)<0,即f(x1)<f(x2)
∴f(x)在(0,+∞)上是增函数. …(9分)
(3)由(2)可知f(x)在(0,+∞)上是增函数,
∴f(x)在[
,2]上是增函数…(10分)
∴f(x)max=f(2)=
,f(x)min=f(
)=-
…(12分)
| 3 |
| 2 |
∴-2a+
| 1 |
| 2 |
| 3 |
| 2 |
得a=1,∴f(x)=x-
| 1 |
| x |
(2)f(x)在(0,+∞)上是增函数
设x1,x2∈(0,+∞),且x1<x2…(4分)
f(x1)-f(x2)=x1-
| 1 |
| x1 |
| 1 |
| x2 |
| (x1-x2)(x1x2+1) |
| x1x2 |
∵0<x1<x2
∴x1-x2<0,x1x2>0,x1x2+1>0…(8分)
∴f(x1)-f(x2)<0,即f(x1)<f(x2)
∴f(x)在(0,+∞)上是增函数. …(9分)
(3)由(2)可知f(x)在(0,+∞)上是增函数,
∴f(x)在[
| 1 |
| 2 |
∴f(x)max=f(2)=
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
点评:本题考查函数的解析式,考查函数的单调性的判断与证明,考查函数的最值,确定函数的单调性是关键.

练习册系列答案
相关题目
定义在(-1,1)上的函数f(x)-f(y)=f(
);当x∈(-1,0)时f(x)>0.若P=f(
)+f(
),Q=f(
),R=f(0);则P,Q,R的大小关系为( )
| x-y |
| 1-xy |
| 1 |
| 5 |
| 1 |
| 11 |
| 1 |
| 2 |
| A、P<Q<R |
| B、R<Q<P |
| C、R<P<Q |
| D、Q<P<R |
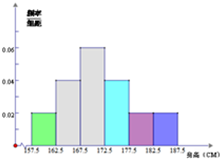 云南省2014年全省高中男生身高统计调查数据显示:全省100000名男生的身高服从正态分布N(107.5,16).现从我校高三年级男生中随机抽取50名测量身高,测量发现被测学生身高全部介于157.5cm和187.5cm之间,将测量结果按如下方式分成6组:第一组[157.5,162.5],第二组[162.5,167.5],…,第6组[182.5,187.5],如图是按上述分组方法得到的频率分布直方图.
云南省2014年全省高中男生身高统计调查数据显示:全省100000名男生的身高服从正态分布N(107.5,16).现从我校高三年级男生中随机抽取50名测量身高,测量发现被测学生身高全部介于157.5cm和187.5cm之间,将测量结果按如下方式分成6组:第一组[157.5,162.5],第二组[162.5,167.5],…,第6组[182.5,187.5],如图是按上述分组方法得到的频率分布直方图.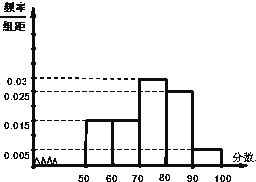 高二年级从参加期末考试的学生中抽出60名学生,并统计了他们的物理成绩(成绩均为整数且满分为100分),把其中不低于50分的分成五段[50,60),[60,70)…[90,100]后画出如下部分频率分布直方图.观察图形的信息,回答下列问题:
高二年级从参加期末考试的学生中抽出60名学生,并统计了他们的物理成绩(成绩均为整数且满分为100分),把其中不低于50分的分成五段[50,60),[60,70)…[90,100]后画出如下部分频率分布直方图.观察图形的信息,回答下列问题: