题目内容
若f(x)是定义在(0,+∞)上的增函数,且对一切x,y>0,满足f(
)=f(x)-f(y)
(1)求f(1)的值,
(2)若f(6)=1,解不等式f(x+3)-f(
)<2.
| x |
| y |
(1)求f(1)的值,
(2)若f(6)=1,解不等式f(x+3)-f(
| 1 |
| 3 |
考点:抽象函数及其应用,函数单调性的性质
专题:函数的性质及应用
分析:(1)利用赋值法即可求f(1)的值,
(2)若f(6)=1,结合抽象函数将不等式f(x+3)-f(
)<2进行转化,结合函数的单调性解不等式即可.
(2)若f(6)=1,结合抽象函数将不等式f(x+3)-f(
| 1 |
| 3 |
解答:
解:(1)在f(
)=f(x)-f(y)中,
令x=y=1,则有f(1)=f(1)-f(1),
∴f(1)=0;
(2)∵f(6)=1,∴2=1+1=f(6)+f(6),
∴不等式f(x+3)-f(
)<2
等价为不等式f(x+3)-f(
)<f(6)+f(6),
∴f(3x+9)-f(6)<f(6),
即f(
)<f(6),
∵f(x)是(0,+∞)上的增函数,
∴
,解得-3<x<9,
即不等式的解集为(-3,9).
| x |
| y |
令x=y=1,则有f(1)=f(1)-f(1),
∴f(1)=0;
(2)∵f(6)=1,∴2=1+1=f(6)+f(6),
∴不等式f(x+3)-f(
| 1 |
| 3 |
等价为不等式f(x+3)-f(
| 1 |
| 3 |
∴f(3x+9)-f(6)<f(6),
即f(
| x+3 |
| 2 |
∵f(x)是(0,+∞)上的增函数,
∴
|
即不等式的解集为(-3,9).
点评:本题主要考查抽象函数的应用,根据函数单调性将不等式进行转化是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知O为△ABC外一点,D为BC边上一点,且
+
-2
=0,若AB=3,AC=5.则
•
=( )
| OC |
| OB |
| OD |
| AD |
| BC |
| A、-8 | B、8 | C、-2 | D、2 |
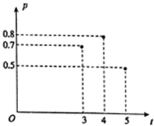 加工爆米花时,爆开且不糊的粒数占加工总粒数的百分比称为“可食用率”,在特定条件下,可食用率p与加工时间t(单位:分钟)满足下列某函数关系:①p=at+b②p=alogbt③p=at2+bt+c(a,b,c是常数),如图记录了三次实验的数据,
加工爆米花时,爆开且不糊的粒数占加工总粒数的百分比称为“可食用率”,在特定条件下,可食用率p与加工时间t(单位:分钟)满足下列某函数关系:①p=at+b②p=alogbt③p=at2+bt+c(a,b,c是常数),如图记录了三次实验的数据,