题目内容
6.在正方体ABCDD一A1B1C1D1中,点E为线段C1D1上一点,且满足$\frac{{D}_{1}E}{E{C}_{1}}$=$\sqrt{3}$+1,则直线AB1与直线CE所成的角的大小为( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
分析 以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,利用向量法能求出直线AB1与直线CE所成的角的大小.
解答 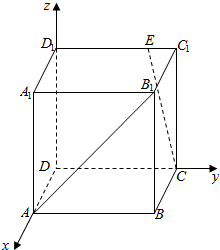 解:以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,
解:以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,
设正方体ABCDD一A1B1C1D1中棱长为$\sqrt{3}+2$,
则A($\sqrt{3}+2$,0,0),B1($\sqrt{3}+2,\sqrt{3}+2,\sqrt{3}+2$),
C(0,$\sqrt{3}+2$,0),E(0,$\sqrt{3}+1$,$\sqrt{3}+2$),
$\overrightarrow{A{B}_{1}}$=(0,$\sqrt{3}+2,\sqrt{3}+2$),$\overrightarrow{CE}$=(0,-1,$\sqrt{3}+2$),
设直线AB1与直线CE所成的角为θ,
则cosθ=$\frac{|\overrightarrow{A{B}_{1}}•\overrightarrow{CE}|}{|\overrightarrow{A{B}_{1}}|•|\overrightarrow{CE}|}$=$\frac{5+3\sqrt{3}}{\sqrt{14+8\sqrt{3}}•\sqrt{8+4\sqrt{3}}}$=$\frac{5+3\sqrt{3}}{10+6\sqrt{3}}$=$\frac{1}{2}$,
∴θ=60°.
∴直线AB1与直线CE所成的角的大小为60°.
故选:C.
点评 本题考查异面直线所成角的大小的求法,是基础题,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
相关题目
17.点E、F分别是三棱锥P-ABC的棱AP、BC的中点,AB=6,PC=8,EF=5,则异面直线AB与PC所成的角为( )
| A. | 60° | B. | 45° | C. | 30° | D. | 90° |
14.若函数$f(x)=sinωx-\sqrt{3}cosωx$,ω>0,x∈R,又f(x1)=2,f(x2)=0,且|x1-x2|的最小值为$\frac{3π}{2}$,则ω的值为( )
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{4}{3}$ | D. | 2 |
1.已知$\overrightarrow i$和$\overrightarrow j$是互相垂直的单位向量,向量$\overrightarrow{a_n}$满足:$\overrightarrow i•\overrightarrow{a_n}=n$,$\overrightarrow j•\overrightarrow{a_n}=2n+1$,n∈N*,设θn为$\overrightarrow i$和$\overrightarrow{a_n}$的夹角,则( )
| A. | θn随着n的增大而增大 | B. | θn随着n的增大而减小 | ||
| C. | 随着n的增大,θn先增大后减小 | D. | 随着n的增大,θn先减小后增大 |