题目内容
17．点E、F分别是三棱锥P-ABC的棱AP、BC的中点，AB=6，PC=8，EF=5，则异面直线AB与PC所成的角为（ ）| A． | 60° | B． | 45° | C． | 30° | D． | 90° |
分析 取AC中点O，连结EO、FO，∠EOF为异面直线AB与PC所成的角或所成角的补角，由此能求出异面直线AB与PC所成的角的大小．
解答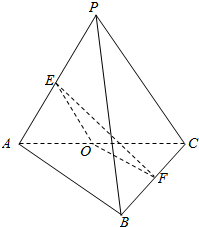 
解：如图，取AC中点O，连结EO、FO，
∵E、F分别是三棱锥P-ABC的棱AP、BC的中点，AB=6，PC=8，EF=5，
∴EO∥PC，且EO=$\frac{1}{2}PC$=4，
FO∥AB，且FO=$\frac{1}{2}AB$=3，
∴∠EOF为异面直线AB与PC所成的角或所成角的补角，
∵EO2+FO2=EF2，
∴∠EOF=90°．
∴异面直线AB与PC所成的角为90°．
故选：D．
点评 本题考查异面直线所成角的大小的求法，是基础题，解题时要认真审题，注意空间思维能力的培养．
练习册系列答案
名校课堂系列答案
相关题目
8．在平面直角坐标系xOy中，已知点A（0，-1），B点在直线y=1上，M点满足$\overrightarrow{MB}$∥$\overrightarrow{OA}$，$\overrightarrow{MA}$•$\overrightarrow{AB}$=$\overrightarrow{MB}$•$\overrightarrow{BA}$，M点的轨迹方程为（ ）
| A． | y2=4x | B． | x2=-4y | C． | x2+4y2=1 | D． | x2-4y2=1 |
12．甲、乙两名运动员在某项测试中的6次成绩的茎叶图如图所示，${\overline{x}}_{1}$，${\overline{x}}_{2}$分别表示甲、乙两名运动员这项测试成绩的平均数，s${\;}_{1}^{2}$，s${\;}_{2}^{2}$分别表示甲、乙两名运动员这项测试成绩的方差，则有（ ）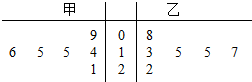
| A． | ${\overline{x}}_{1}$＞${\overline{x}}_{2}$，s${\;}_{1}^{2}$＜${s}_{2}^{2}$ | B． | ${\overline{x}}_{1}$=${\overline{x}}_{2}$，s${\;}_{1}^{2}$＞${s}_{2}^{2}$ | ||
| C． | ${\overline{x}}_{1}$=${\overline{x}}_{2}$，s${\;}_{1}^{2}$=${s}_{2}^{2}$ | D． | ${\overline{x}}_{1}$=${\overline{x}}_{2}$，s${\;}_{1}^{2}$＜${s}_{2}^{2}$ |