题目内容
1．已知$\overrightarrow i$和$\overrightarrow j$是互相垂直的单位向量，向量$\overrightarrow{a_n}$满足：$\overrightarrow i•\overrightarrow{a_n}=n$，$\overrightarrow j•\overrightarrow{a_n}=2n+1$，n∈N*，设θn为$\overrightarrow i$和$\overrightarrow{a_n}$的夹角，则（ ）| A． | θn随着n的增大而增大 | B． | θn随着n的增大而减小 | ||
| C． | 随着n的增大，θn先增大后减小 | D． | 随着n的增大，θn先减小后增大 |
分析 分别以 $\overrightarrow i$和$\overrightarrow j$所在的直线为x轴，y轴建立坐标系，则$\overrightarrow i$=（1，0），$\overrightarrow{j}$=（0，1），设$\overrightarrow{a_n}$=（xn，yn），进而可求出tanθn，结合函数的单调性即可判断．
解答 解：分别以 $\overrightarrow i$和$\overrightarrow j$所在的直线为x轴，y轴建立坐标系，则$\overrightarrow i$=（1，0），$\overrightarrow{j}$=（0，1），
设$\overrightarrow{a_n}$=（xn，yn），
∵$\overrightarrow i•\overrightarrow{a_n}=n$，$\overrightarrow j•\overrightarrow{a_n}=2n+1$，n∈N*，
∴xn=n，yn=2n+1，n∈N*，
∴$\overrightarrow{a_n}$=（n，2n+1），n∈N*，
∵θn为$\overrightarrow i$和$\overrightarrow{a_n}$的夹角，
∴tanθn=$\frac{{y}_{n}}{{x}_{n}}$=$\frac{2n+1}{n}$=2+$\frac{1}{n}$
∴y=tanθn为减函数，
∴θn随着n的增大而减小．
故选：B．
点评 本题主要考查了向量的数量积的坐标表示，解题的关键是根据已知条件把所求问题坐标化．
练习册系列答案
名校课堂系列答案
相关题目
12．甲、乙两名运动员在某项测试中的6次成绩的茎叶图如图所示，${\overline{x}}_{1}$，${\overline{x}}_{2}$分别表示甲、乙两名运动员这项测试成绩的平均数，s${\;}_{1}^{2}$，s${\;}_{2}^{2}$分别表示甲、乙两名运动员这项测试成绩的方差，则有（ ）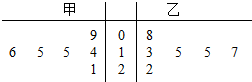
| A． | ${\overline{x}}_{1}$＞${\overline{x}}_{2}$，s${\;}_{1}^{2}$＜${s}_{2}^{2}$ | B． | ${\overline{x}}_{1}$=${\overline{x}}_{2}$，s${\;}_{1}^{2}$＞${s}_{2}^{2}$ | ||
| C． | ${\overline{x}}_{1}$=${\overline{x}}_{2}$，s${\;}_{1}^{2}$=${s}_{2}^{2}$ | D． | ${\overline{x}}_{1}$=${\overline{x}}_{2}$，s${\;}_{1}^{2}$＜${s}_{2}^{2}$ |
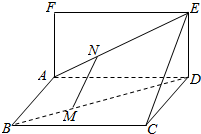如图，已知矩形ABCD和矩形ADEF所在平面互相垂直，点M，N分别在对角线BD、AE上，且BM=$\frac{1}{3}$BD，AN=$\frac{1}{3}$AE，求证：MN∥平面CDE．