题目内容
(1)已知f(x)=
,g(x)=(x-e)2+
,x>0,求f(x)的最大值;比较f(x)与g(x)的大小并说明理由.
(2)已知函数f(x)=tanx-x,0<x<
,证明:当0<x<
时,tanx>x.
| lnx |
| x |
| 1 |
| e |
(2)已知函数f(x)=tanx-x,0<x<
| π |
| 2 |
| π |
| 2 |
考点:利用导数求闭区间上函数的最值
专题:导数的综合应用
分析:(1)由已知得f′(x)=
,x>0,由此利用导数性质能推导出g(x)≥f(x),当且仅当x=e时取等号.
(2)由已知得f′(x)=(
)′-1=
-1=
>0,由此利用导数性质能证明当0<x<
时,tanx>x.
| 1-lnx |
| x2 |
(2)由已知得f′(x)=(
| sinx |
| cosx |
| cos2x+sin2x |
| cos2x |
| sin2x |
| cos2x |
| π |
| 2 |
解答:
(1)解:f′(x)=
,x>0,
当0<x<e时,f′(x)>0,
当x>e时,f′(x)<0,且f′(e)=0,
所以f(x)max=f(x)极大值=f(e)=
,即f(x)≤
,
而g(x)=(x-e)2+
≥
,
故g(x)≥f(x),当且仅当x=e时取等号.
(2)证明:f′(x)=(
)′-1=
-1=
>0,
所以函数f(x)在区间(0,
)上为增函数,而x>0,
所以f(x)>f(0)=tan0-0=0,
故当0<x<
时,tanx>x.
| 1-lnx |
| x2 |
当0<x<e时,f′(x)>0,
当x>e时,f′(x)<0,且f′(e)=0,
所以f(x)max=f(x)极大值=f(e)=
| 1 |
| e |
| 1 |
| e |
而g(x)=(x-e)2+
| 1 |
| e |
| 1 |
| e |
故g(x)≥f(x),当且仅当x=e时取等号.
(2)证明:f′(x)=(
| sinx |
| cosx |
| cos2x+sin2x |
| cos2x |
| sin2x |
| cos2x |
所以函数f(x)在区间(0,
| π |
| 2 |
所以f(x)>f(0)=tan0-0=0,
故当0<x<
| π |
| 2 |
点评:本题考查两式大小的比较,考查不等式的证明,是中档题,解题时要认真审题,注意导数性质的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
函数f(x)=xlnx在点x=1处的导数为( )
| A、-1 | B、0 | C、1 | D、2 |
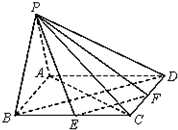 如图,在四棱锥P-ABCD中,四边形ABCD是菱形,PB=PD,且EF分别是BC,CD的中点.求证:
如图,在四棱锥P-ABCD中,四边形ABCD是菱形,PB=PD,且EF分别是BC,CD的中点.求证: