题目内容
已知函数f（x）的定义域为（-∞，0）∪（0，+∞）的奇函数，在区间（0，+∞）上单调递增，且f（-2）=0，若f（x）＜0，则x的取值范围是 ．
考点：函数奇偶性的性质
专题：函数的性质及应用
分析：首先，根据函数为奇函数，得到在区间（-∞，0）上单调递减，然后，利用f（-2）=0，得到f（2）=0，从而得到相应的结果．
解答：
解：∵函数f（x）奇函数，在区间（0，+∞）上单调递增，
∴在区间（-∞，0）上单调递减，
∵f（-2）=0，
∴f（2）=0，
∴当x＜-2时，f（x）＜0，
当-2＜x＜0时，f（x）＞0，
当0＜x＜2时，f（x）＜0，
当x＞0时，f（x）＞0，
∴当x＜-2或0＜x＜2时，f（x）＜0，
故答案为：（-∞，-2）∪（0，2）．
∴在区间（-∞，0）上单调递减，
∵f（-2）=0，
∴f（2）=0，
∴当x＜-2时，f（x）＜0，
当-2＜x＜0时，f（x）＞0，
当0＜x＜2时，f（x）＜0，
当x＞0时，f（x）＞0，
∴当x＜-2或0＜x＜2时，f（x）＜0，
故答案为：（-∞，-2）∪（0，2）．
点评：本题重点考查了函数为奇函数，奇函数的概念和图象特征等知识，属于中档题．
练习册系列答案
相关题目
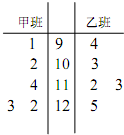为了解甲、乙两个班级某次考试的数学成绩，从甲、乙两个班级中分别随机抽取5名学生的成绩（单位：分）作样本，如图是样本的茎叶图：
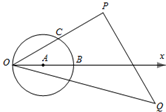如图，在极坐标系中，设极径为ρ（ρ＞0），极角为θ（0≤θ＜2π），⊙A的极坐标方程为ρ=2cosθ，点C在极轴的上方，∠AOC=m=2是复数（m-2）+（m2-3m+2）i（m∈R）是纯虚数的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分且必要条件 |
| D、既不充分也不必要条件 |