题目内容
已知命题P:?x∈(-∞,0),2x<3x;命题q:?a>0函数f(x)=ln2x+lnx-a有零点.则下列命题为真命题的是( D )( )
| A、p∧q |
| B、p∨(¬q) |
| C、p∧(¬q) |
| D、(¬p)∧q |
考点:复合命题的真假
专题:函数的性质及应用,简易逻辑
分析:运用图象判断判断命题P:?x∈(-∞,0),2x<3x,是假命题.函数f(x)=ln2x+lnx-a有零点,lnx∈(-∞,+∞),
得出1+4a≥0,a≥-
,命题q“?a>0函数f(x)=ln2x+lnx-a”有零点是真命题.运用复合命题的真假问题.
得出1+4a≥0,a≥-
| 1 |
| 4 |
解答:
解:画出图象y=2x,y=3x,可判断命题P:?x∈(-∞,0),2x<3x,是假命题.
¬p为真命题,

∵函数f(x)=ln2x+lnx-a有零点,lnx∈(-∞,+∞)
∴1+4a≥0,a≥-
,
∴命题q“?a>0函数f(x)=ln2x+lnx-a”有零点是真命题.
¬q为假命题.
∴(¬p)∧q是真命题.
故选:D
¬p为真命题,

∵函数f(x)=ln2x+lnx-a有零点,lnx∈(-∞,+∞)
∴1+4a≥0,a≥-
| 1 |
| 4 |
∴命题q“?a>0函数f(x)=ln2x+lnx-a”有零点是真命题.
¬q为假命题.
∴(¬p)∧q是真命题.
故选:D
点评:本题考查了函数的图象和性质,复合命题的真假,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
圆锥的母线长为6,轴截面的顶角为120度,过两条母线作截面,则截面面积的最大值为( )
A、9
| ||
| B、18 | ||
C、18
| ||
| D、9 |
下列函数中,在其定义域上为减函数的是( )
A、y=x
| ||
B、y=(
| ||
| C、y=sinx | ||
| D、y=log2x |
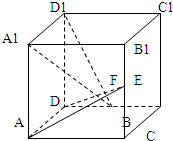 如果正方体ABCD-A1B1C1D1中EF分别是BB1、CD中点.
如果正方体ABCD-A1B1C1D1中EF分别是BB1、CD中点.