题目内容
2.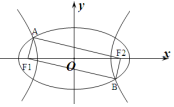 如图F1、F2是椭圆C1:$\frac{{x}^{2}}{4}$+y2=1与双曲线C2的公共焦点,A、B分别是C1、C2在第二、四象限的公共点,若四边形AF1BF2为矩形,则C2的离心率是( )
如图F1、F2是椭圆C1:$\frac{{x}^{2}}{4}$+y2=1与双曲线C2的公共焦点,A、B分别是C1、C2在第二、四象限的公共点,若四边形AF1BF2为矩形,则C2的离心率是( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{6}}{2}$ |
分析 设|AF1|=x,|AF2|=y,利用椭圆的定义,四边形AF1BF2为矩形,可求出x,y的值,进而可得双曲线的几何量,即可求出双曲线的离心率.
解答 解:设|AF1|=x,|AF2|=y,
∵点A为椭圆C1:$\frac{{x}^{2}}{4}$+y2=1上的点,
∴2a=4,b=1,c=$\sqrt{3}$;
∴|AF1|+|AF2|=2a=4,即x+y=4;①
又四边形AF1BF2为矩形,
∴$|A{F}_{1}{|}^{2}+|A{F}_{2}{|}^{2}=|{F}_{1}{F}_{2}{|}^{2}$,
即x2+y2=(2c)2=12,②
由①②得x=2-$\sqrt{2}$,y=2+$\sqrt{2}$.
设双曲线C2的实轴长为2a′,焦距为2c′,
则2a′=|AF2|-|AF1|=y-x=2$\sqrt{2}$,2c′=2$\sqrt{3}$,
∴C2的离心率是e=$\frac{c′}{a′}$=$\frac{\sqrt{3}}{\sqrt{2}}=\frac{\sqrt{6}}{2}$,
故选:D.
点评 本题考查椭圆与双曲线的简单性质,求得|AF1|与|AF2|是关键,考查分析与运算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.已知集合I={x∈Z|-3<x<3},A={-2,0,1},B={-1,0,1,2},则(∁IA)∩B等于( )
| A. | {-1} | B. | {2} | C. | {-1,2} | D. | {-1,0,1,2} |
17.函数f(x)=x+$\frac{1}{2x}$,x∈($\frac{1}{2}$,2),若f(x)-m>0对一切x∈($\frac{1}{2}$,2)恒成立,则实数m的取值范围为( )
| A. | (-∞,$\frac{\sqrt{2}}{2}$) | B. | (-∞,$\sqrt{2}$) | C. | (-∞,$\frac{3}{2}$) | D. | ($\frac{3}{2}$,$\frac{9}{4}$) |
7.集合M={x|0<x≤3},N={x|0<x≤2},则a∈M是a∈N的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
14.某电影公司2012年大陆电影票房为21亿元,若该公司大陆电影票房的年平均增长率为x,2016年大陆电影票房为y亿元,则y与x的函数关系式为( )
| A. | y=84x | B. | y=21(1+4x) | C. | y=21x4 | D. | y=21(1+x)4 |