题目内容
已知x＞0，y＞0，且（x-1）（y-1）≥2，则x+y的取值范围是（ ）
| A、[3，+∞） | ||
| B、[2，+∞） | ||
C、[2
| ||
D、[
|
考点：基本不等式
专题：不等式的解法及应用
分析：由题意结合基本不等式可得关于x+y的不等式，解不等式可得．
解答：
解：∵x＞0，y＞0，且（x-1）（y-1）≥2，
∴xy-x-y+1≥2，即x+y+1≤xy，
由基本不等式可得x+y+1≤xy≤(
)2，
整理可得（x+y）2-4（x+y）-4≥0，
解得x+y≥2+2
，或x+y≤2-2
，
∵x＞0，y＞0，∴舍去x+y≤2-2
，
∴x+y的取值范围为：[2+2
，+∞）
故选：C
∴xy-x-y+1≥2，即x+y+1≤xy，
由基本不等式可得x+y+1≤xy≤(
| x+y |
| 2 |
整理可得（x+y）2-4（x+y）-4≥0，
解得x+y≥2+2
| 2 |
| 2 |
∵x＞0，y＞0，∴舍去x+y≤2-2
| 2 |
∴x+y的取值范围为：[2+2
| 2 |
故选：C
点评：本题考查基本不等式和一元二次不等式的解法，属基础题．
练习册系列答案
相关题目
某单位有若干部门，现召开一个70人的座谈会，决定用分层抽样的方法从各部门选取代表，其中一个部门20人中被抽取4人，则这个单位应有（ ）
| A、200人 | B、250人 |
| C、300人 | D、350人 |
用反证法证明：“若a，b，c都是正数，则三个数a+
，b+
，c+
中至少有一个不小于2”时，“假设”应为（ ）
| 1 |
| b |
| 1 |
| c |
| 1 |
| a |
A、假设a+
| ||||||
B、假设a+
| ||||||
C、假设a+
| ||||||
D、假设a+
|
设f（x）=x2-2x-4lnx，则f（x）的增区间为（ ）
| A、（0，+∞） |
| B、（2，+∞） |
| C、（-∞，-1） |
| D、（∞，-1）和（2，+∞） |
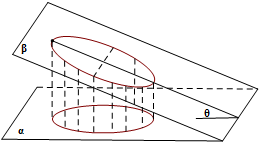如图，一个底面半径为R的圆柱被与其底面所成角为θ（00＜θ＜900）的平面所截，截面是一个椭圆．当θ为30°时，这个椭圆的离心率为（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、
|