题目内容
已知数列{an}与{bn}满足bn=2an(n∈N*),数列{bn}是等比数列,且b1+b5=68,a2+a4=8.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若数列{bn}是递增数列,设cn=an+bn,求数列{cn}的前n项和Sn.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若数列{bn}是递增数列,设cn=an+bn,求数列{cn}的前n项和Sn.
考点:数列的求和
专题:等差数列与等比数列
分析:(Ⅰ)由等差数列和等比数列的性质结合已知得到b1,b5的值,进一步得到a1,a5的值,然后求出等差数列的公差,则数列{an}的通项公式可求;
(Ⅱ)由数列{bn}是递增数列得到其通项公式,然后分别利用等差数列和等比数列的前n项和求得数列{cn}的前n项和Sn.
(Ⅱ)由数列{bn}是递增数列得到其通项公式,然后分别利用等差数列和等比数列的前n项和求得数列{cn}的前n项和Sn.
解答:
解:(Ⅰ)∵a2+a4=8,
∴b2b4=2a2•2a4=2a2+a4=256.
又数列{bn}是等比数列,
∴b1b5=b2b4=256.
又已知b1+b5=68,
故b1,b5是一元二次方程x2-68x+256=0的两根.
则
或
易知数列{an}是等差数列,
当
时,
,
则数列{an}的公差d=
=1.
故an=a1+(n-1)d=2+(n-1)×1=n+1;
当
时,
,
则数列{an}的公差d=
=-1.
故an=a1+(n-1)d=6+(n-1)×(-1)=7-n.
综上,数列{an}的通项公式为an=n+1或an=7-n;
(Ⅱ)若数列{bn}是递增数列,由(Ⅰ)得an=n+1,bn=2n+1.
∴cn=an+bn=(n+1)+2n+1.
∴Sn=(a1+b1)+(a2+b2)+…+(an+bn)=(a1+a2+…+an)+(b1+b2+…+bn)
=[2+3+…+(n+1)]+(22+23+…+2n+1)
=
+
=
+2n+2-4.
∴b2b4=2a2•2a4=2a2+a4=256.
又数列{bn}是等比数列,
∴b1b5=b2b4=256.
又已知b1+b5=68,
故b1,b5是一元二次方程x2-68x+256=0的两根.
则
|
|
易知数列{an}是等差数列,
当
|
|
则数列{an}的公差d=
| a5-a1 |
| 4 |
故an=a1+(n-1)d=2+(n-1)×1=n+1;
当
|
|
则数列{an}的公差d=
| a5-a1 |
| 4 |
故an=a1+(n-1)d=6+(n-1)×(-1)=7-n.
综上,数列{an}的通项公式为an=n+1或an=7-n;
(Ⅱ)若数列{bn}是递增数列,由(Ⅰ)得an=n+1,bn=2n+1.
∴cn=an+bn=(n+1)+2n+1.
∴Sn=(a1+b1)+(a2+b2)+…+(an+bn)=(a1+a2+…+an)+(b1+b2+…+bn)
=[2+3+…+(n+1)]+(22+23+…+2n+1)
=
| n(2+n+1) |
| 2 |
| 22(1-2n) |
| 1-2 |
| n(n+3) |
| 2 |
点评:本题考查了等差数列和等比数列的性质,考查了等差数列和等比数列的前n项和,是中档题.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
从6本不同的数学书和5本不同的英语书中取3本,要求数学书和英语书都要有取到,则不同的取法种数有( )种.
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
函数y=cos2x-sin2x 的一条对称轴为( )
A、x=
| ||
B、x=
| ||
C、x=-
| ||
D、x=-
|
(x+1)5展开式的二项式系数的和是( )
| A、6 | B、128 | C、32 | D、64 |
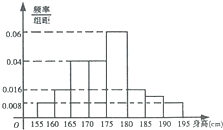 从某校高三年级800名学生中随机抽取50名测量身高,据测量,被抽取的学生的身高全部介于155cm和195cm之间,将测量结果按如下方式分成八组:第一组[155,160),第二组[160,165),…,第八组[190,195],如图是按上述分组方法得到的频率分布直方图:
从某校高三年级800名学生中随机抽取50名测量身高,据测量,被抽取的学生的身高全部介于155cm和195cm之间,将测量结果按如下方式分成八组:第一组[155,160),第二组[160,165),…,第八组[190,195],如图是按上述分组方法得到的频率分布直方图: