题目内容
已知关于x的一元二次方程x2+(m-3)x+1=0的两根x1和x2满足x1<x2<1.求实数m的取值范围.
考点:二次函数的性质
专题:计算题,函数的性质及应用
分析:设f(x)=x2+(m-3)x+1,利用关于x的一元二次方程x2+(m-3)x+1=0的两根x1和x2满足x1<x2<1,建立不等式组,即可求实数m的取值范围.
解答:
解:设f(x)=x2+(m-3)x+1,
∵关于x的一元二次方程x2+(m-3)x+1=0的两根x1和x2满足x1<x2<1,
∴
,
∴m>5.
∵关于x的一元二次方程x2+(m-3)x+1=0的两根x1和x2满足x1<x2<1,
∴
|
∴m>5.
点评:本题主要考查一元二次方程的根的分布,即考查实根分布问题,解决此类问题的关键是熟练掌握一元二次函数的图象.

练习册系列答案
相关题目
已知一个几何体的正(主)视图与侧(左)视图均为长等于2的正三角形,俯视图如图所示,在俯视图中,半圆的直径与等腰直角三角形的斜边长均为2,则该几何体的体积为( )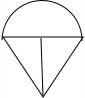

A、
| ||||
B、
| ||||
C、
| ||||
D、
|
